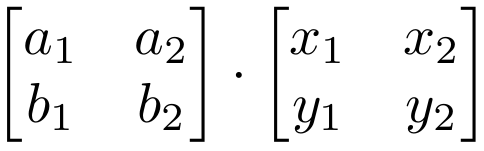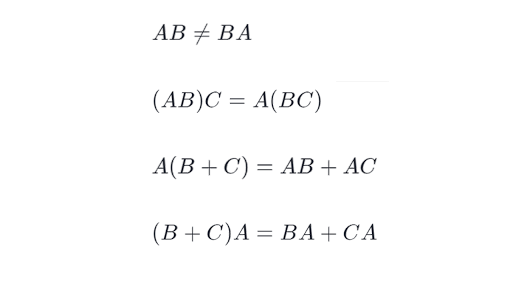If Matrix Multiplication Is Commutative Then
If the product of two symmetric matrices is symmetric then they must commute. The reader is encouraged to find other examples.

Is Matrix Multiplication Commutative Video Khan Academy
There are some exceptions however most notably the identity matrices that is the n by n matrices I_n which consist of 1s along the main diagonal and 0 for all other entries and which act as the multiplicative identity for matrices In general when taking the product of two matrices A and B where A is a matrix with m rows and n.
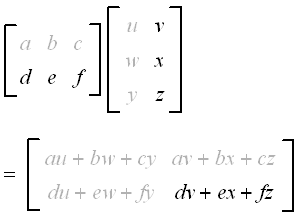
If matrix multiplication is commutative then. And thats the only necessary condition. Commutative law is not valid for multiplication. You can try to perform the multiplication with more than two matrices.
For all x other than 2 and - 2. Multiplication of blocks will give diagonal λ 1 λ 2 first off-diagonal λ 1 λ 2 and second off-diagonal 1 so assuming scalar multiplication and addition is commutative so will the jordan blocks. If the matrix is commutative with the matrix then.
The product BA is defined that is we can do the multiplication but the product when the matrices are multiplied in this order will be 33 not 22. As for a mathematical system in which matrix multiplication is in general commutative I cant think of any besides the trivial set of 1 x 1 matrices. The idea is to write proofs using exactly the properties you need.
Properties of Matrix Multiplication 1. A T F Matrix Multiplication Is Commutative. If the two matrices have Jordan Normal Forms which have the same block structure.
Jordan blocks commute with upper triangular matrices that have the same value along bands. For example this always works when A is the zero matrix or when A B. B T F If Fn 3000n3 And Gn 2n3 Then FnOgn c T F If Fn 0gn Then Gn Ωfn d T F lognOn Vm EZ e T F If Sets A And B Are Countable Then A X B Is Also Countable f T F The Largest 4-digit Number In Base 5 Is 5555 g T.
Every diagonal matrix commutes with all other diagonal matrices. Let is singular matrix. For example if A is an identity matrix Then B can be any matrix with the same dimensions as A.
While matrix multiplication is not commutative in general there are examples of matrices A and B with AB BA. Suppose I had included commutativity of multiplication in the definition of a ring. Well see for instance that matrix multiplication is usually not commutative.
AB BA in general. Similarly the multiplication induced by this successoring is not normal matrix multiplication. Clearly commutative law is true in the case of matrix multiplication if one of the matrix is identity matrix.
ExampleNon-commutative multiplication of matrices. Multiplication of matrices generally is not commutative ie. Thus given matrix is non-singular for all x other than 2 and - 2.
Then if I proved something. In particular matrix multiplication is not commutative. You cannot switch the order of the factors and expect to end up with the same result.
In general matrix multiplication is not commutative. F Consider Functions 1. In that way the things that you prove can be used in a wider variety of situations.
They form a commutative ring since the sum of two circulant matrices is circulant. You will find that the induced multiplication is in fact commutative while of course matrix multiplication is not. First you have to match the orders in such a fashion that A and B are both of the same size and theyre both squared.
So there are two things that are going on.
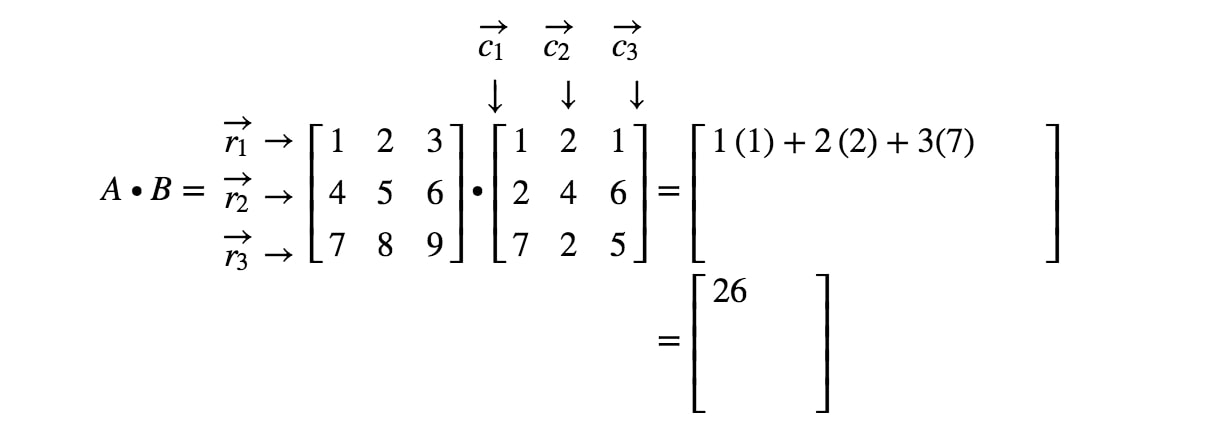
How To Multiply Two Matrices Together Studypug

Consider The Following Set Of Real 2 2 Matrices A Chegg Com

Proof That The Matrix Multiplication Is Associative Is Commutativity Of The Elements Necessary Mathematics Stack Exchange
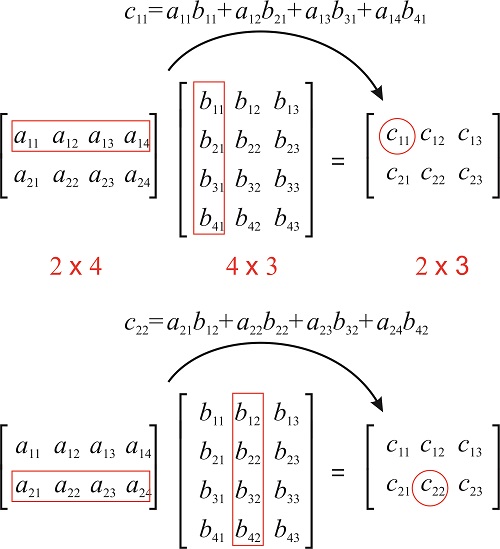
15 3 Matrix Multiplication Chemistry Libretexts

Question Video Possibility Of Commutativity In Matrix Multiplication Nagwa

Question Video Determining Whether Matrix Multiplication Can Be Commutative Under Special Circumstances Nagwa
Matrix Multiplication Calculator

3 4a Matrix Operations Finite Math
Properties Of Matrix Multiplication Article Khan Academy
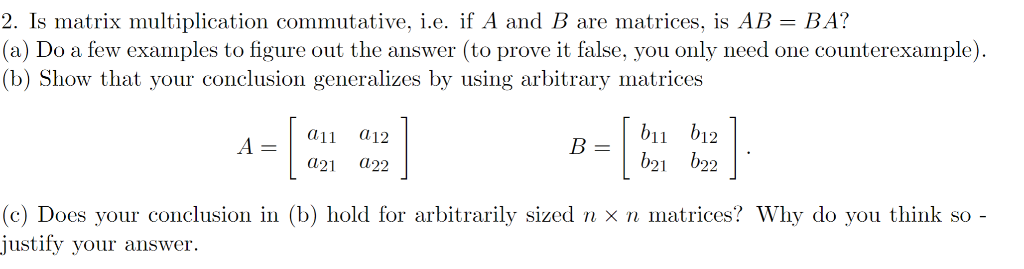
2 Is Matrix Multiplication Commutative I E If A Chegg Com

1 Consider The Following Sets Of Real 2 X 2 Chegg Com

Solved Algebra We Know That Matrix Multiplication Is Not Chegg Com

Commutative Property Of Matrix Multiplication In The Algebra Of Polynomial Mathematics Stack Exchange
Matrix Multiplication Is Not Commutative

3 4a Matrix Operations Finite Math

We Know That Matrix Multiplication Is Not Chegg Com
What Are The Conditions Necessary For Matrix Multiplication Quora