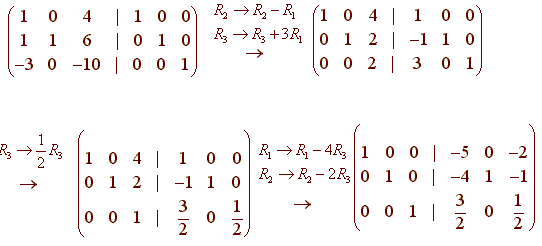Matrix Inverse Properties Proof
3Finally recall that ABT BTAT. Three Properties of the Inverse 1If A is a square matrix and B is the inverse of A then A is the inverse of B since AB I BA.

Inverses Of Matrices And Its Properties Mathematics Stack Exchange
BIf A is invertible and c 6 0 is a scalar then cA is invertible and.

Matrix inverse properties proof. AA-1 A-1A I where I is the Identity matrix. A A AA 0 where 0 is the zero matrix here. Suppose B 1 and B 2 are both inverses of the matrix A.
IfB isthematrixobtainedbyaddingamultipleofanyrowofAtoadifferentrow of A then detB detA. Then we have the identity. BACD BAC gives BI D IC or B D C.
Simply verify that the expression above does indeed satisfy each of the four Penrose conditions. Can a matrix have more than one inverse. Let A and B be matrices with the same dimensions and let k be a number.
Note 2 The matrix A cannot have two different inverses. However since V is an isometry Ax b VDUx b. If A is an invertible matrix then a matrix B is its inverse iff A B I B A.
Otherwise we can write A VDU where U and V are orthogonal. If A is a square matrix then its inverse A 1 is a matrix of the same size. By definition C is the inverse of the matrix B A 1 if and only if B C C B I.
I n is the n n identity matrix. Every nonzero row of rref A contains a leading 1. Thus no nonzero row of rref A can be written as a linear combination of the other rows.
A0 0A A. ProofFirstassumethatA is a rectangular diagonal matrix DasaboveThensincex minimizes Dx b2 iff Dx is the projection of b onto the image subspace F of Ditisfairlyobviousthatx Db. If A is an invertible matrix then its inverse must be unique.
Theorem Properties of matrix inverse. Then S UDUT where D is again a diagonal matrix whose diagonal elements are determined according to Example 3. Let A be an nn matrix.
Suppose BA D I and also AC D I. Lets show an important property of matrix inverses. Properties of Matrices Inverse.
A ATAAT ATAAT 2. TheoremIf Ais invertible then its inverse is unique. Since matrix additionsubtraction amounts to addingsubtracting cor-.
Its diagonal elements are equal to 1 and its o diagonal elements are equal to 0. All entries above and below the leading 1 s are 0. Then B D C according to this proof by parentheses.
The identity matrix for the 2 x 2 matrix is given by. Mn-matrix is given by x Ab UDVb. Suppose by way of contradiction that theinverse of Ais not unique ie let BandCbe two distinct inverses of AThen by defn of inverse.
Let S 2 IRnn be symmetric with UTSU D where U is orthogonal and D is diagonal. Not every square matrix has an inverse. AIf A is invertible then A 1 is itself invertible and A 1 1 A.
The proofs of these properties are given at the end of this section. Therefore you can prove your property by showing that a product of a certain pair of matrices is equal to I. The additive inverse of A is A.
If A is a matrix then is the matrix having the same dimensions as A and whose entries are given by Proposition. Each matrix has an additive inverse. The nonzero rows of rref A are linearly independent.
If B is the matrix obtained by permuting two rows of A then detB detA. If A is a non-singular square matrix there is an existence of n x n matrix A-1 which is called the inverse of a matrix A such that it satisfies the property. Then we have AB 1 B 1AI 14 AB 2 B 2AI 15 Now take the equation AB 1 I.
A 1 1 A 2Notice that B 1A 1AB B 1IB I ABB 1A 1. We denote by 0 the matrix of all zeroes of relevant size. Elimination solves Ax D b without explicitly using the matrix A 1.
Then we have AB 1 B 1AI 14 AB 2 B 2AI 15 Now take the equation AB 1 I. It is noted that in order to find the matrix inverse the square matrix should be non-singular whose determinant value does. Let A be a matrix.
If A is an invertible matrix then its inverse must be unique. For all A 2 IRmn 1. Lets show an important property of matrix inverses.
Note 1 The inverse exists if and only if elimination produces n pivots row exchanges are allowed. If B is the matrix obtained by multiplying one row of A by any2 scalar k then detB k detA. Note that in b the 0 on the left is the number 0 while the 0 on the right is the zero matrix.
Suppose B 1 and B 2 are both inverses of the matrix A. Therefore by Theorem thredundantifflindep of VEC-M-0100 the. If we denote this matrix by 0 then it has the following property.
AB 1 B 1A 1 Then much like the transpose taking the inverse of a product reverses the order of the product.

Inverses Of Matrices And Its Properties Mathematics Stack Exchange

Chap 2 Matrices 2 1 Operations With Matrices Ppt Video Online Download

Linear Algebra Chapter 2 Matrices 2 1 Addition

Linear Algebra Lecture 25 The Invertible Matrix Theorem Youtube

Linear Algebra 63 Properties Of Matrix Transpose Proofs Youtube

Properties Of Inverses Of Matrices Definition Theorem Formulas Solved Example Problems Inverse Of A Non Singular Square Matrix

Matrices And Determinants Powerpoint Slides

Properties Of Inverses Of Matrices Definition Theorem Formulas Solved Example Problems Inverse Of A Non Singular Square Matrix

Inverse Of A Matrix Advanced Higher Maths

Properties Of The Inverse Matrix

202 6a Transpose Of The Inverse Youtube
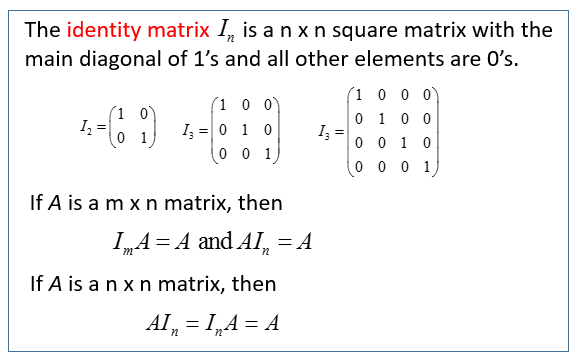
Zero Identity And Inverse Matrices Solutions Examples Videos Worksheets Games Activities
Can Non Square Matrices Have Inverses Quora

Chap 2 Matrices 2 1 Operations With Matrices Ppt Video Online Download

How To Prove The Inverse Of The Matrix Quora

Matrix Inverse Properties Youtube

Chap 2 Matrices 2 1 Operations With Matrices Ppt Video Online Download