Matrix Multiplication With Index Notation
Contrasting 1 and 2 we notice that the k index in 1 corresponds to the BC product and the k index in 2 corresponds to the AB product. 531 To get the element in the ith row and jth column of the product BA take the scalar product of the ith row-vector of Bwith the j-th column vector of A.
Pin On Spm
712 Matrix Notation.
Matrix multiplication with index notation. V and index notation. Alternative notations X X i X i X i XN i1 X i are used when we want to be explicit about the index over which the summation is per-formed or the. B1 b2 b3 9.
If a vector X either a row or column vector has N components then X X i stands for X 1 X 2 X 3 X N. Then substitute the first line in for d s entry. The index notation for these equations is.
The matrix multiplication then remains as a contraction between an upper and a lower pair of indices. I suspect that some of them dont even understand that theyre just using the definition of matrix multiplication. We show how to use index notation and sum over row and column indices to perform matrix multiplication.
Einstein Summation Crash Course PDF. BikAkj in the summation convention. B 3 ca 3.
The resulting language seems easy to use. The rule for matrix multiplication is. 133 Sigma Notation Sigma notation is used as a shorthand way of writing sums.
The abstract way to write a matrix multiplication with indices. The next line is multiplication in index notation with n o and p taking place of the dummy indices of i k and j respectively. I or simply.
One free index as here indicates three separate equations. IjtobeanRPmatrixThematrixproductAB isde ned onlywhenRNandistheMPmatrixCc ijgivenby c ij XN k1 a ikb kj a i1b1j a i2b2j a iNb Nk Usingthesummationconventionthiscanbewrittensimply c ij a ikb kj wherethesummationisunderstoodtobeovertherepeatedindexkInthecaseofa33 matrixmultiplyinga3 1columnvectorwehave 2 6 4 a11 a12 a13 a21 a22 a23 a31 a32 a33 3 7 5 8. This formula uses the kj entry of the matrix product BC which is BC_ kj sum_m B_ k m C_ m j.
Make the inner index k in this case the same and sum over it Example. Property of tensor notation namely that the indices dictate the summation and order of multiplication not the order in which the terms are written. The implied summation over repeated indices without the presence of an explicit sum sign is called Einstein summation and is commonly used in both matrix and tensor analysis.
The trace of a matrix is de ned to be the sum of its diagonal elements TrC X i C ii 12 We would like to prove that TrAB TrBA 13 2. We need to argue that 1 and 2 are equal. The index i is called a j free index.
N-way generalization of matrix notation Summary The capabilities of matrix notation and algebra are generalized to n-way arrays. I i j ij b a x ρ σ 7111 Note the dummy index. Httpsamznto2IDWxaOEinstein Summation Crash Course.
Begineqnarray C BA C_ij mathop _k12B_ ikA_kjquad text B_ikA_kj in the summation convention 531 endeqnarray. The next line is multiplication for E and C and then substitute the second line for e s entry. The symbolic notation.
The Einstein summation convention is introduced. 3 It is simple to see that the index i is incremented between 1 and 3 in equation 3 and the multiplication is. The area of a triangle bounded on.
B 1 ca 1. All the capabilities of matrix notation are retained and most carry over naturally to the n-way context. So people who use the index notation a lot but never write any for all statements tend to think of a notation like Amu_rho as representing a matrix rather than a matrix element.
If one term has a free index i then to be consistent all terms must have it. The abstract way to write a matrix multiplication with indices. For example one can multiply.
For later it is. Multiplication of a matrix by a number is called scalar multiplication. In addition to the suggestion of walber97 Id also propose that the transpose should not lower or raise indices.
Let us look at scalar-vector multiplication in indicial notation. The product of two matrices and is defined as 1 where is summed over for all possible values of and and the notation above uses the Einstein summation convention. It just interchanges the order of the indices.
B 2 ca 2. Ca b b 1 b 2 b 3 ca 1 ca 2 ca 3 2 ca i b i. Trace of a product of matrices.
Finding All Real Eigenvalues Of A 3 X 3 Matrix Maths Exam Algebra Math Videos
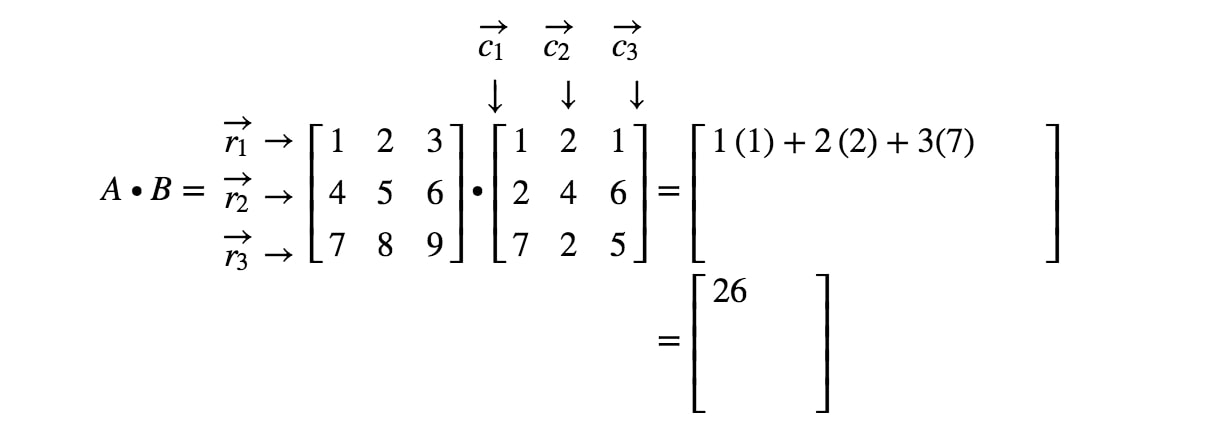
How To Multiply Two Matrices Together Studypug
Pin By Ian On It S Math Studying Math College Math Learning Mathematics
Pin On Teacher Teaching
Pin On Tutor In Physics Math
How To Multiply Matrices By Scalars Studypug
Pin On Rd Sharma Solutions
How To Multiply Two Matrices Together Studypug
The Identity Matrix Rewritten As A Summation Index Notation Youtube
Matrix Multiplication From Wolfram Mathworld
A Complete Beginners Guide To Matrix Multiplication For Data Science With Python Numpy By Chris The Data Guy Towards Data Science
Pin On Math
Pin On Competitive Test Questions Solutions Guidelines Tutorials Maths On Ssccgl Wbcs Bankpo
How To Multiply Two Matrices Together Studypug
Pin On Images
Applied Mechanics Of Solids A F Bower Appendix C Index Notation
Matrix Multiplication Refer To This Video By Mathispower4u By Solomon Xie Linear Algebra Basics Medium
Pin On Maths
Multiplication Of Matrix An Overview Sciencedirect Topics
