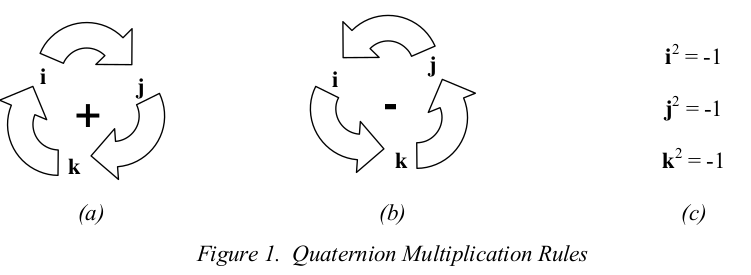
Multiplying Quaternions Product
Another important way to multiply a pair of quaternions involves first taking the transpose of one of the quaternions. Quatprod quatmultiply qr calculates the quaternion product quatprod for two quaternions q and r.
Quaternion
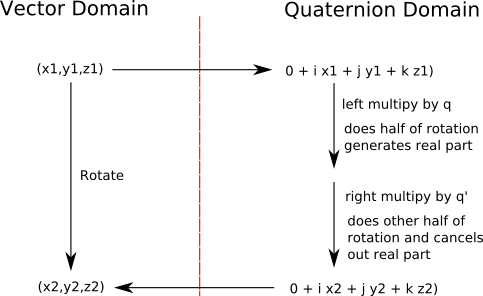
Rotating by the product lhs rhs is the same as applying the two rotations in sequence.
Multiplying quaternions product. For a real-valued matrix representation this is equivalent to multiplication by the transpose which involves flipping the sign of the 3-vector. Multiplying two quaternions together has the effect of performing one rotation around an axis and then performing another rotation about around an. AB cD ac BDaD Bc BxD.
The dot product gi. The Quaternion Multiplication q q1 q2 calculator computes the resulting quaternion q from the product of two q1 and q2. Another important way to multiply a pair of quaternions involves first taking the conjugate of one of the quaternions.
1 Multiplying Quaternions the Easy W ay Multiplying two complex numbers a b I and c d I is straightforward. Multiply Quaternion Quaternion Returns the quaternion that results from multiplying two quaternions together. Here is how we multiply two quaternions together using Python.
In Quaternion maths multiplying by the inverse is the equivalent of subtracting the rotation. The most important operations upon vectors include the dot and cross products and are indispensable for doing physics and vector calculus. Enter the scalar q 4 and i j and k components q 1 q 2 q 3 of quaternion one.
So multiplication of two quaternions combines the rotations just as multiplying matrices does eg. Legend has it thatHamilton was walking with his wife Helen at the Royal Irish Academy when he was suddenlystruck by the idea of adding a fourth dimension in order to multiply triples. For more information on the quaternion forms see Algorithms.
The development of quaternions is attributed to W. Excited by thisbreakthrough as the couple passed the Broome Bridge of the Royal Canal he carved the newfoundquaternion equations. Puzzle Check that this formula gives the same result for quaternion multiplication as the explicit rules for multiplying i j and k.
Aerospace Toolbox uses quaternions that are defined using the scalar-first convention. The Quaternions We can use the cross product and the dot product. Why we use quaternions.
Multiplication of quaternions is like complex numbers but with the addition of the cross product. Lhs first and then rhs relative to the reference frame resulting from lhs rotation. Yes thats correct.
The requirement that we can represent subsequent rotations by multiplying the quaternion I turns out that this is the only mapping between quaternions and the position of a point on a rotating object is this sandwich product. Note that this means rotations are not commutative so lhs rhs does not give the same rotation as rhs lhs. Aerospace Blockset uses quaternions that are defined using the scalar-first convention.
V0vw0w v0w0 vw. For a real-valued matrix representation this is equivalent to multiplication by the conjugate which involves flipping the sign of the 3-vector. That is to say that if C A inverse B then C B A.
This is explained for quaternions on this page and more generally on this page. In OpenGL glRotate function. The Euclidean Inner and Outer Products.
Form the Euclidean inner product. The Quaternion Multiplication block calculates the product for two given quaternions. Doing that you will get a formula equivalent to the Euler-Rodrigues Formula.
A nice thing is that multiplication of two normalized quaternions again produces a normalized quaternion. Multiplication of a quaternion q by its inverse q 1 results in the multiplicative identity 1 0 0 0. A unit-length quaternion also referred to here as a unit quaternion ˆq is created by dividing each of the four components by the square root of the sum of the squares of those components Eq.
V v 2 r x s v r x v m where x represents the cross product s and r are the scalar and vector parts of the quaternion respectively and m is the sum of the squares of the components of the quaternion. Ab cd ac bdad bc For two quaternions b I and d I become the 3-vectors B and D where B x I y J z K and similarly for D. Vw v1w1 v2w2 v3w3 to define the product of quaternions in yet another way.
Maths Quaternion Transforms Martin Baker
Explaining How Quaternions A Four Dimensional Number System Describe 3d Rotation Number System Visual Rotating
Pin On Mathematics
Hamilton S Quaternions And 3d Rotation With Python Meccanismo Complesso
Quaternions Basics Gps
Quaternions As 4x4 Matrices Connections To Linear Algebra Youtube Algebra Equations Algebra Math Formulas
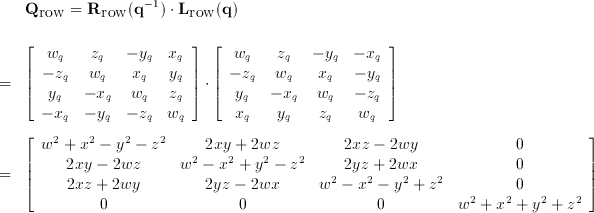
Cs184 Using Quaternions To Represent Rotation
Lecture 9 6 837 Fall 01
Quaternions
Maths Quaternion Transforms Martin Baker
Let S Remove Quaternions From Every 3d Engine Intro To Rotors From Geometric Algebra Geometric Algebra Algebra How To Remove
Pin On Math
Unit Quaternion Description Of Spatial Rotation In 3d Electron Cryo Microscopy Biorxiv
Cs184 Using Quaternions To Represent Rotation
Pin On Robo
Quaternion Multiplication Multiplication Interactive Number System
John Carlos Baez On Twitter The Beauty Of Quaternion Multiplication Is That It Combines All Ways Of Multiplying Scalars And Vectors In A Single Package And Obeys Ab A B Last
Understanding Quaternions Physics And Mathematics Distance Time Graphs Worksheets Logic Math
Quaternion Multiplication
