Property Of Skew Symmetric Matrix Proof
A matrix is symmetric if and only if it is equal to its transpose. Similarly in characteristic different from 2 each diagonal element of a skew-symmetric matrix must be zero since each is its own negative.

Ppt Symmetric And Skew Symmetric Matrices Powerpoint Presentation Free Download Id 2646318
Then letting J 0 1 10 we have A4n θ4nI 2 A4n1 θ4n1J.

Property of skew symmetric matrix proof. Let A be a square matrix then we can write A 12 A A 12 A A. We have a theorem says that ODD-SIZED SKEW-SYMMETRIC MATRICES ARE SINGULAR. Or Take a Test.
Since it follows that is symmetric. Q T -Q. A 1 2 43 2 1-2 -3 2.
Det A T det -A -1 n detA The inverse of skew-symmetric matrix does not exist because the determinant of it having odd order is zero and hence it is singular. These properties are widely used in Lyapunov-based stability proofs and are therefore important to identify. Skew Symmetric Matrix Properties.
Every square diagonal matrix is symmetric since all off-diagonal elements are zero. Now let us assume we have a 3 3 skew symmetric matrices of the form 0 a 3 a 2 a 3 0 a 1 a 2 a 1 0 and an Identity matrix I 3 3. In linear algebra a real symmetric matrix represents a self-adjoint operator over a real inner product space.
Prove that every Hermitian matrix A can be written as the sum ABiC where B is a real symmetric matrix and C is a real skew-symmetric matrix. In this video I explained class 12 Math chapter 3 matrices symmetric matrices skew symmetric matrices theoremsMπKstudyMithileshsymmetricMatrixskewSymm. In other words a square matrix Q which is equal to negative of its transpose is known as skew-symmetric matrix ie.
X ij -x ji for all values of i and j. Express a Hermitian Matrix as a Sum of Real Symmetric Matrix and a Real Skew-Symmetric Matrix Recall that a complex matrix is called Hermitian if AA where AbarAtrans. If n is odd then detA 0 for any n x n skew-symmetric matrixThanks for watching.
For any ntimes n matrix A and a scalar c we have detAdetAtrans detcAcndetA. Skew symmetric matrix is a square matrix Q x ij in which i j th element is negative of the j i th element ie. The second equality follows from the fact that A is symmetric so and B is symmetric so.
As an example let us compute the exponential of the real skew symmetric matrix A 0 θ θ 0. B The sum of skew symmetric matrices is skew symmetric. We will use the following two properties of determinants of matrices.
A Let A and B be symmetric. Definition Skew-Symmetric A matrix A is called skew-symmetric if Atrans-A. Using Theorem 3 we square both sides of eq.
I must show that is symmetric. All main diagonal entries of a skew-symmetric matrix. So you just want to show that if CTransposeBSB then TranposeC-C.
Symmetric property of the Coriolis matrix for vehicle-manipulator systems. Use up and down arrows to select. 0 suggestions are available.
Now The first equality follows from a property I proved for transposes. We need to find an inductive formula expressing the powers An. Themappingu u isbyinspectionlinearandinvertible.
1 Properties of skew symmetric matrices 1. 13 to obtain pfBMBT 2 pf M2detB2. Here Atrans is the transpose of A.
Prove that A A T is a symmetric and A A T is a skew symmetric matrix where. 19 Using the well known properties of determinants it follows that detBMBT detMdetB2. I must show that is skew symmetric.
If A is a skew-symmetric matrix which is also a square matrix then the determinant of A should satisfy the below condition. A matrix is skew symmetric if that condition holds. Proof link is given here if needed.
From the Theorem 1 we know that A A is a symmetric matrix and A A is a skew-symmetric matrix. All entries above the main diagonal of a symmetric matrix are reflected into equal entries below the diagonal. For example the skew-symmetric property does not depend on the system at hand but on the choice of parameterisation of the Coriolis matrix which is not unique.
If Mis a complex antisymmetric matrix then detM pf M2. Any Square matrix can be expressed as the sum of a symmetric and a skew-symmetric matrix. A matrix is skew-symmetric if and only if it is the opposite of its transpose.
Now use TransposeS-S. Eigenvalue of Skew Symmetric Matrix. Since for any matrix A kA kA it follows that 1 2 AA is a symmetric matrix and 1 2 A A is a skew-symmetric matrix.
First we assume that M is a non-singular complex 2n 2nantisymmetric matrix. B Let A and B be skew symmetric so and. Let us observe that 0 θ θ 0 θ 0 1 10 and 0 θ θ 0 2 θ2 10 01.
U v 2 4 u 2v 3 u 3v 2 u 3v 1 u 1v 3 u 1v 2 u 2v 1 3 5 1 Fromtheequalityaboveonecanseethatthefollowingskewsymmetricmatrix u 2 4 0 u 3 u 2 u 3 0 u 1 u 2 u 1 0 3 5 2 satisfiesu v u v.

Proof If N Is Odd Then Det A 0 For Skew Symmetric Matrix Youtube

Symmetric And Skew Symmetric Matrices Definition Theorem Solved Example Problems

Symmetric And Skew Symmetric Ppt Video Online Download

What Is Determinant Of Skew Symmetric Matrix
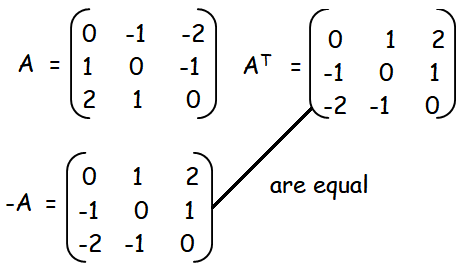
Questions On Symmetric And Skew Symmetric Matrix
What Is A Skew Symmetric Matrix Quora

Class 12 Symmetric And Skew Symmetric Matrices Youtube

Does The Set Of Skew Symmetric N N Matrices Form A Vector Space With The Usual Matrix Addition And Scalar Multiplication Quora

Mathematics Symmetric Skew Symmetric And Orthogonal Matrix Youtube

Symmetric And Skew Symmetric Matrices Lecture 6 Youtube

What Is The Determinant Of Every Skew Symmetric Matrix Quora

Derivative Of A Rotation Matrix Robot Academy

Symmetric And Skew Symmetric Ppt Video Online Download

Derivative Of A Rotation Matrix Robot Academy

What Form Does A 3 3 Matrix Have If It Is Symmetric As Well As Skew Symmetric Quora

Ppt Symmetric And Skew Symmetric Matrices Powerpoint Presentation Free Download Id 2646318

Linear Algebra 91 Skew Symmetric Proofs Youtube

Cbse Class 12 Symmetric And Skew Symmetric Matrices Elementary Operations And Invertible Matrices Offered By Unacademy

Problem 1 An N X N Complex Matrix A Is Called Chegg Com