Symmetric Matrix Eigenvalues Singular Values
Now we look for the maximum and the minimum value of this quadratic form subject to the constraint that mathbfx1. Hence this is respectively the largest and the smallest eigenvalue of the symmetric matrix ATA.

Singular Value Decomposition Svd For Non Symmetric Square Real Matrix Contradicts Spectral Theorem Mathematics Stack Exchange
We will study somebasic results and techniques.

Symmetric matrix eigenvalues singular values. In fact we can compute that the eigenvalues are p 1 360 2 90 and 3 0. Therefore the singular values of G M-112BKD 2 are the square roots of the eigenvalues of K and the left singular vectors of G are the eigenvectors of K as shown in Theorem 33. It turns out that singular vectors can always be chosen to.
The singular values of A are assumed to be nonnegative and sorted to satisfy 12 n 0. The eigenvalues of A are real to see this suppose Av λv v 6 0 v Cn then vTAv vTAv λvTv λ Xn i1 vi2 but also vTAv Av T v λv T v λ Xn i1 vi2. PA LU Guassian Elimination A QR Gram-Schmidt A S S 1 and when A is symmetric A Q QT.
And a number C is an eigenvalue of A precisely when L 0 ie when 0 and thus A I is singular. If A is a symmetric matrix the singular values are the absolute values of the eigenvalues of A. All eigenvalues of a real symmetric matrix are real.
Relation to Eigenvalues For Hermitian symmetric matrices there is no fundamental di erence between the SVD and eigenvalue decompositions. It is easily seen that. To show these two properties we need to considercomplex matrices of typeA2Cnn whereCis the set ofcomplex numberszxiywherepxandyare the realand imaginary part of zandi 1.
Note that G is nonzero only on the main diagonal and on the first superdiagonal. Finding bounds and estimates of eigenvalues singular valuesand diagonal entries of matrices are important in many applications. Thus the singular values of Aare 1 360 6 p 10 2 p 90 3 p 10 and 3 0.
Nthe singular values are precisely the positive parts of the eigenvalues of A ordered in decreasing order since the construction above gives 2 i to be the eigenvalues of A TA A2. 103 eigshow The function eigshow is available in the Matlab demos directory. Important class are the symmetric matrices whose eigenvectors form an orthogonal basis of Rn.
In their place one uses the square roots of the eigenvalues of the associated square Gram matrix K ATA which are called singular values of the original matrix. We know that at least one of the eigenvalues is 0 because this matrix can have rank at most 2. This method employs an initial orthogonal factorization using block Householder transformations and then determines the singular values and singular vectors of the.
Eigenvectors corresponding to distinct eigenvalues areorthogonal. A non-square matrix A does not have eigenvalues. A nal word about SVD for symmetric matrices.
Eigenvalues and Singular Values An important matrix factorization is the famous SVD A U VTIt joins our other important factorizations. Sponding symmetric tridiagonal matrix. If in addition A is a symmetric positive definite matrix then U V Sigma are square non-singular matrices.
Eigenvalues and Singular Values A First Course in Numerical Methods - Uri M. Therefore λ 2 is an eigenvalue for P P which is the square of a singular value for the matrix P. Ascher Chen Greif All the textbook answers and step-by-step explanations Get certified as an expert in up to 15 unique STEM subjects this summer.
Sigma_ilambda_i and the columns of UV are the eigenvectors of A. Eigenvalues of symmetric matrices suppose A Rnn is symmetric ie A AT fact. Here Σ is a matrix the same size as A that is zero except possibly on its main diagonal.
It is called the characteristic polynomial of the matrix A. Such matrices are called bidiagonal and most. Real mn matrix with mn.
This is a quadratic form whose matrix is equal to ATA. The squared singular values are eigenvalues of the normal matrix. Here are some facts about eigenvalues and singular values.
3 and the singular values 817 247 and 0003. The input to eigshow is a real 2-by-2 matrix A or you can choose an A from a pull-down list. Similarly the singular vectors are the corresponding eigenvectors up to a sign.
The matrix in a singular value decomposition of Ahas to be a 2 3 matrix so it must be 6 p 10 0 0 0 3 p 10 0. Recall that the singular valuess1A snA ofAMnare the nonnegative squareroots of the eigenvalues ofAA. If the matrix Ais symmetric hence square and has eigenvalues 1.
This matrix is symmetric since. DetA I is a nth-degree polynomial of the form 1 0 1 ˆ 1 ˆˆ n n n n. Multiply both sides of this equation by P to get P P v P λ v.
IN this sense SVD can be regarded as a. Since P is positive definite λ 0 and hence λ 2 λ. We have P P and hence P P v λ 2 v.
In linear algebra the singular value decomposition SVD is a factorization of a real or complex matrix Aof the form U VH where Uis an m mreal or complex unitary matrix is an m nrectangular diagonal matrix with non-negative real numbers on the diagonal and V is n nreal or complex unitary matrix. This is related in a way that we will make more precise later to the fact that this example is very far from being a symmetric matrix. Eigenvalue and Singular Value Decompositions 3 Written in matrix form the defining equations for singular values and vectors are AV UΣ AHU VΣH.
IA p iAA p iAA since AA VUUV V 2V. In Section 5 we present a multiprocessor scheme for determining the SVD of an m Xn-matrix in which m n or n m. Its zeros are the eigenvalues of A.
The numerical computation of eigenvalues. Let A USV T 21 be an SVD of A where U uu1 m is an mm orthogonal matrix V vv1 n is an nn or- thogonal matrix and S diag 1 n is an mn diagonal matrix.
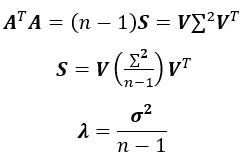
Singular Value Decomposition And Its Applications In Principal Component Analysis By Mohamed Afham Towards Data Science

Singular Vector An Overview Sciencedirect Topics

Singular Values And Vectors Of Symmetric Matrices Mathematics Stack Exchange

5 Symmetric Positive Definite Matrices Have Only Chegg Com

Eigen Decomposition And Singular Value Decomposition Ppt Video Online Download

Eigen Decomposition And Singular Value Decomposition Based On

Eigen Decomposition And Singular Value Decomposition Based On

Eigen Decomposition And Singular Value Decomposition Ppt Video Online Download

Linear Algebra For Communications A Gentle Introduction Ppt Download

Eigen Decomposition And Singular Value Decomposition Based On

Eigen Decomposition And Singular Value Decomposition Ppt Video Online Download

Chapter 4 The Eigen Decomposition Of A Symmetric Matrix Isn T Always Its Svd Issue 218 Mml Book Mml Book Github Io Github
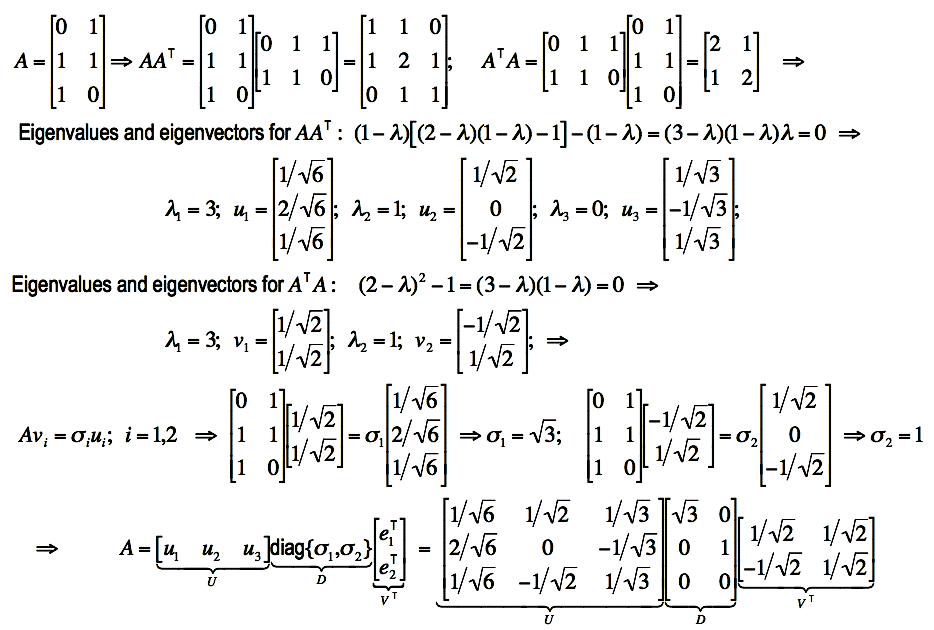
Compsci773s1t Vision Guided Control

Eigen Decomposition And Singular Value Decomposition Based On

Term Document Matrices And Singular Value Decompositions
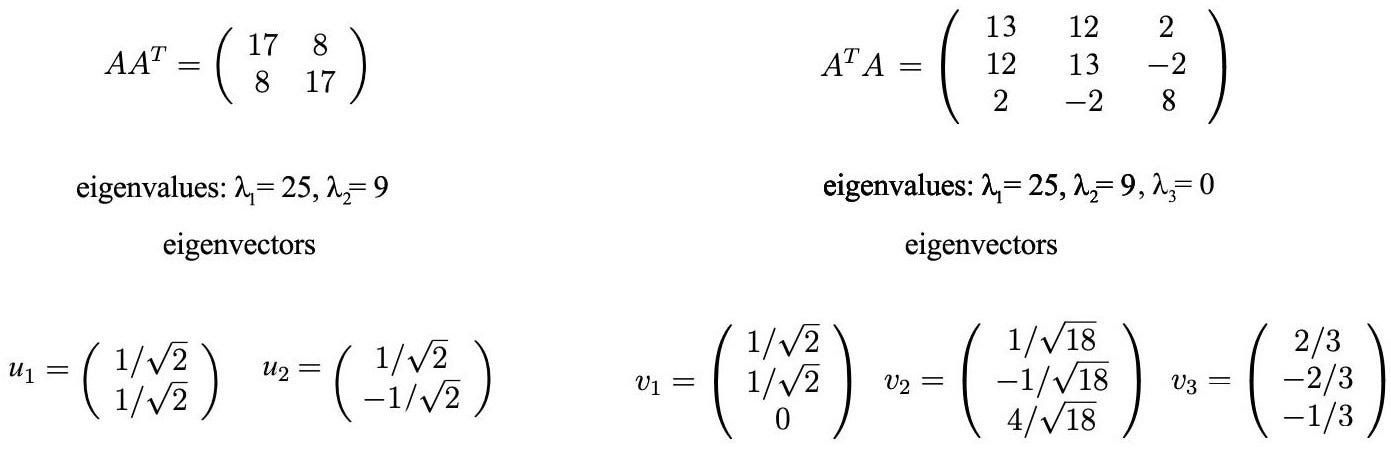
Machine Learning Singular Value Decomposition Svd Principal Component Analysis Pca By Jonathan Hui Medium

Visualization Of Singular Value Decomposition Of A Symmetric Matrix Mathematics Stack Exchange

Solved Problem 3 20 Points Eigenvalues And Singular Val Chegg Com

A 3x3 Symmetric Eigenvalue Decomposition In Under 3 Minutes Youtube