The Matrix Has No Multiplicative Inverse

03 Apr, 2021

Furthermore does the given matrix have a multiplicative inverse explain your answer. Look at the numbers.

Pin On Algebra 2

The multiplicative inverse of a matrix is similar in concept except that the product of matrix latexAlatex and its inverse latexA-1latex equals the identity matrix.

The matrix has no multiplicative inverse. Set the matrix must be square and append the identity matrix of the same dimension to it. Where I is the identity matrix made up of all zeros except on the main diagonal which contains all 1. The multiplicative inverse of a matrix A is a matrix indicated as A1 such that.

This means A B B A I A C C A. This means if you row reduce to try to compute the inverse one of the rows will have only zeros which means there is no inverse. Wow theres a lot of similarities there between real numbers and matrices.

If the determinant is 0 the matrixhas no inverse. In math symbol speak we have A A sup. Similarly not every matrix has an inverse.

A square matrix is singular only when its determinant is exactly zero. Next transpose the matrixby rewriting the first row as the first column the middle row as the middle column and the third row as the third column. If a square matrix has a multiplicative inverse that is if the matrix is nonsingular then that inverse is unique.

Reduce the left matrix to row echelon form using elementary row operations for the whole matrix including the right one. This is where the Identity Matrix. No the matrix is square and square matrices do not have multiplicative inverses.

Thats good right - you dont want it to be something completely different. The Inverse of a Matrix Over the set of real number we have what we call the multiplicative inverse or reciprocal. The identity matrix is a square matrix containing ones down the main diagonal and zeros everywhere else.

Such a matrix is called Singular which only happens when the determinant is zero. Yes because there is no column of all zeros. The second row is just double the first row and does not add any new information.

This Matrix has no Inverse. The inverse of a square matrix A denoted by A -1 is the matrix so that the product of A and A -1 is the Identity matrix. A matrix X is invertible if there exists a matrix Y of the same size such that where is the n -by- n identity matrix.

The multiplicative inverse of a number is a second number that when multiplied by the first number yields the multiplicative identity 1. What we noticed however was that this could be a time consuming process. C is a group and the proof of unicity of the inverse of a matrix is the same proof in any group.

A matrix that has no inverse is singular. And the determinant lets us know this fact. So the number 0 has no multiplicative inverse.

In Inverse Matrix we saw that we were able to find the multiplicative inverse or show that no such inverse existed by augmenting the matrix with the identity matrix and row reducing. When talking about a matrix with or without an inverse the following terminology is used. This matrix has no inverse because the columns are not linearly independent.

Assume that there exists two inverses of A. A A1 A1 A I. For it to even be a possibility the matrix must first be square same number of rows as columns.

If a determinant of the main matrix is zero inverse doesnt exist. And it makes sense. The matrix Y is called the inverse of X.

The multiplicative inverse of a matrix is the matrix that gives you the identity matrix when multiplied by the original matrix. As a result you will get the inverse calculated on the right. Even then there may not be an inverse.

Let A a given invertible matrix and denote B and C two inverses of A. Multiplicative inverse of the matrix Sec1 Algebra Unit 1 Last lesson. The identity matrix that results will be the same size as the matrix A.

Pin On Math

Question Video Finding The Inverse Of A Matrix Nagwa

Pin On How To Submit For Fashion Magazines Now

Multiplicative Inverses Of Matrices And Matrix Equations Video Lesson Transcript Study Com

What Is An Inverse Matrix Mathbootcamps

4 5 2x2 Matrices Determinants Inverses Objectives Evaluating Determinants Of 2x2 Matrices Using Inverse Matrices To Solve Equations Ppt Download

Pin On Math Aids Com

Inverse Matrix Explanation Examples

Question Video Finding The Inverse Of A Matrix Nagwa

Question Video Finding The Inverse Of A Diagonal Matrix Nagwa

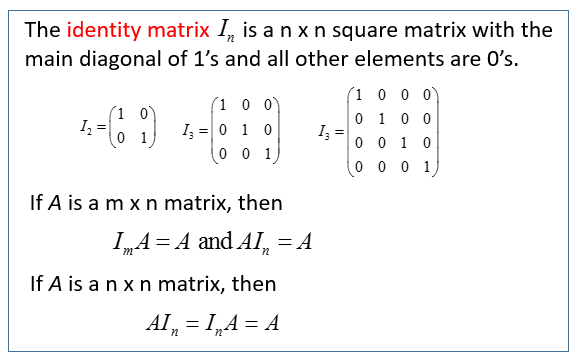
Zero Identity And Inverse Matrices Solutions Examples Videos Worksheets Games Activities

Multiplicative Inverse Of A Matrix Determinant Of A 2x2 Matrix

Multiplicative Inverses Of Matrices And Matrix Equations Video Lesson Transcript Study Com

Multiplying Matrices Self Grading Assessment With Google Forms No Prep And Paperless Rigorous Assess Multiplying Matrices Matrix Multiplication Assessment

Question Video Checking Whether A Matrix Is Invertible Nagwa

Multiplicative Inverse An Overview Sciencedirect Topics

2 5 Determinants And Multiplicative Inverses Of Matrices Objectives 1 Evaluate Determinants 2 Find The Inverses Of Matrices 3 Solve Systems Of Equations Ppt Download

Section 6 2 Matrix Multiplication Inverses And Determinants There Are Three Basic Matrix Operations 1 Matrix Addition 2 Scalar Multiplication 3 Matrix Ppt Download