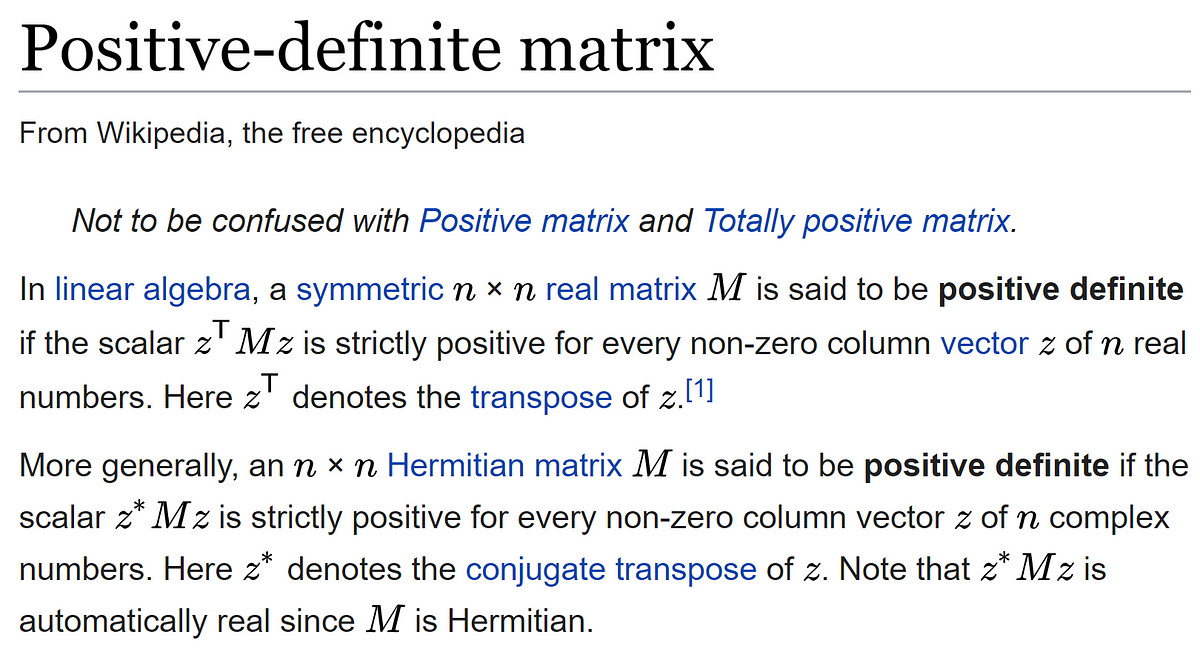
Symmetric Matrices Definition Statistics

14 May, 2021

For every real symmetric matrix A there exists an orthogonal matrix Q and a diagonal matrix dM such that A QT dM Q. Only a square matrix is symmetric because in linear algebra equal matrices have equal dimensions.

Pin On Math Online Learning Education

It is often hard to interpret this abstract property about matrices in the physical or geometrical world but it generally has something to do with symmetry.

Symmetric matrices definition statistics. N values for which px 0. Throughout we assume that all matrix entries belong to a field whose characteristic is not equal to 2. Symmetric Matrix A matrix is called a symmetric matrix if its transpose is equal to the matrix itself.

If a symmetric matrix is rotated by 90 it. Here are three symmetric matrices. That is we assume that 1 1 0 where 1 denotes the multiplicative identity and 0 the additive identity of the given fieldIf the characteristic of the field is 2 then a skew-symmetric matrix is the same thing as a.

A skew symmetric matrix is equal to the negation of its transpose. B B. How do you know if a matrix is symmetric.

Furthermore the entries that are not on the diagonal come in pairs on opposite sides of the diagonal. Definition A matrix A is symmetric if and only if A AT. The entries of a symmetric matrix are symmetric with respect to the main diagonal.

A symmetric matrix is a matrix whose values are symmetric in the northwest-to-southeast diagonal. This decomposition is called a spectral decomposition of A since Q consists of the eigenvectors of A and the diagonal elements of dM are corresponding eigenvalues. Formally matrix A is symmetric if Because equal matrices have equal dimensions only square matrices can be symmetric.

Symmetric square matrices composed of quaternions H H ij n ij1. In fact if r1 rn are the n roots then the polynomial can be expressed as an x ri. The first definition of persymmetric requires that for all i j.

A symmetric matrix and skew-symmetric matrix both are square matrices. Clearly such a matrix is square. Av_122bv_1v_2cv_220 7 for all vv_1v_20.

D x y x A y x T A y. The task is to find a. Its distribution is invariant under conjugation by the symplectic group and it models Hamiltonians with time-reversal symmetry but no rotational symmetry.

By the fundamental theorem of algebra any nth degree polynomial px has exactly n roots ie. If we set X to be the column vector with x k 1 and x i 0 for all i k then X T AX a kk and so if A is positive definite then a kk. Two examples of symmetric matrices appear below.

A diagonal matrix D has numbers along the main diagonal and zeros everywhere else. Symmetric Matrix Skew Symmetric Matrix. For example 5 5 persymmetric matrices are of the form.

A real symmetric matrix A is positive definite iff there exists a true square matrix M such. A A. A matrix A is skew-symmetric if and only if A AT.

If the transpose of a matrix is equal to itself that matrix is said to be symmetric. In other words A is symmetrical about the diagonal. But the difference between them is the symmetric matrix is equal to its transpose whereas skew-symmetric matrix is a matrix whose transpose is equal to its negative.

A symmetric matrix is positive definite if and only if its quadratic form is a strictly convex function. A symmetric matrix is a square matrix that is equal to its transpose. In Exercise 5 you are asked to show that any symmetric or.

Mathematics maths a square matrix that is equal to its transpose being symmetrical about its main diagonal. On the space of n n Hermitian quaternionic matrices eg. AMMT 5 where MT is that the transpose Ayres 1962 p.

An n n symmetric matrix A is positive definite if for any n 1 column vector X 0 X T AX 0. The matrix is skew-symmetric because. If A is a symmetric matrix then A A T and if A is a skew-symmetric matrix then A T A.

This can be equivalently expressed as AJ JA T where J is the exchange matrix. B c 6 is positive definite if. This is because by definition for real vectors x y d x y d y x for all x y and x 2 x T A x 0 for x 0.

A symmetric matrix A has equal numbers in the off-diagonal locations. A is positive semidefinite if for any n 1 column vector X X T AX 0. Especially a 22 symmetric matrix a b.

Let A a i j be an n n matrix. A symmetric matrix is a matrix A such that AT A. A suitable definition of symmetric matrices from first principles is that for any symmetric matrix A AAT.

Note that if A a ij and X x i then. 1 0 0 3 0 1 0 1 5 8 0 8 7 a b c b d e c e f Here are three nonsymmetric. Also symmetric strictly positive definite matrices are the only set of matrices which can define a non-trivial inner product along with an induced norm.

Symmetric And Skew Symmetric Matrix Theorems Videos And Examples