Applications Of Matrix Chain Multiplication
No of Scalar multiplication in Case 2 will be. In other words no matter how we parenthesize the product the result will be the same.
Matrix Chain Multiplication
What are the real world examples of matrix chain multiplication.
Applications of matrix chain multiplication. The positions E i are the states of the chain and. One application you can relate to easily is that of perspective projections which is the foundation for 3D animation. 1 and a transition matrix to be a square matrix each of whose rows is a probability vector.
Here you will learn about Matrix Chain Multiplication with example and also get a program that implements matrix chain multiplication in C and C. Given a sequence of matrices the goal is to find the most efficient way to multiply these matrices. We know that to multiply two matrices it is condition that number of columns in first matrix should be equal to number of rows in second matrix.
The Chain Matrix Multiplication Problem Given dimensions corresponding to matr 5 5 5 ix sequence 5 5 5 where has dimension determinethe multiplicationsequencethat minimizes the number of scalar multiplications in computing. In this example you can learn some concepts such a. That is determine how to parenthisize.
In this video I am gonna share you guys one matrices multiplication application of Markov Chain example. Matrix Chain Multiplication with C Program Example Matrix chain multiplication or Matrix Chain Ordering Problem MCOP is an optimization problem that can be solved using dynamic programming. We can have several ways to multiply the given number of matrices because the matrix multiplication is associative.
Possible Combination of Parentheses in a Matrix Chain Application. The chain matrix multiplication problem involves the question of determining the optimal sequence for performing a series of operations. To find the best possible way to calculate the product we could simply parenthesis the expression in every possible fashion and count each time how many scalar multiplication are required.
Matrix multiplication allows you to convert between 2D and 3D. We then dene a nite Markov chain or simply a chain to consist of an nn transition matrix P and a 1n row vector x. Matrix Chain Multiplication Problem can be stated as find the optimal.
This is the link. For example if we had four matrices A B C and D we would have. Weve discussed Matrix Chain Multiplication using Dynamic Programming in our last article ver clearly.
I have studied matrix chain multiplication wherein given a sequence of matrices the goal is to find the most efficient way to multiply matrices. This is the link. The chain matrix multiplication problem is perhaps the most popular example of dynamic programming used in the upper undergraduate course or review basic issues of dynamic programming in advanced algorithms class.
We all know that matrix multiplication is associativeAB BA in nature. We need to compute M ij 0 i j 5. That is the reason why I am tasked to make a.
100 x 10 x 5 10 x 5 x 50 5000 2500 7500. For example say there are five matrices. The problem is not actually to perform the multiplications but merely to decide the sequence of the matrix multiplications involved.
The matrices have size 4 x 10 10 x 3 3 x 12 12 x 20 20 x 7. In this article we are going to implement it in. Basically what is seen on the computer screen is a 2D picture representing a point in 3D space.
Let us proceed with working away from the diagonal. ABCD AB CD A BCD. All Possible Groupings in a Matrix Chain Application.
We are given the sequence 4 10 3 12 20 and 7. Matrix Chain Multiplication is a method in which we find out the best way to multiply the given matrices. The problem is not actually to perform the multiplications but merely to decide the sequence of the matrix multiplications involved.
Example of Matrix Chain Multiplication. Matrix Chain Multiplication is one of the optimization problem which is widely used in graph algorithms signal processing and network industry 1 4. We have many options to multiply a chain of matrices because matrix multiplication is associative.
100 x 10 x 5 10 x 5 x 50 5000 2500 7500. We know M i i 0 for all i. There must be millions of applications.
In the Chain Matrix Multiplication Problem the fundamental choice is which smaller parts of the chain to calculate first before combining them together. Actually in this algorithm we dont find the final matrix after the multiplication. So we have a lot of orders in which we want to perform the multiplication.
One application you can relate to easily is that of perspective projections which is the foundation for 3D animation. Before going to main problem first remember some basis. We compute the optimal solution for the product of 2 matrices.
I have studied matrix chain multiplication wherein given a sequence of matrices the goal is to find the most efficient way to multiply matrices.
Matrix Chain Multiplication
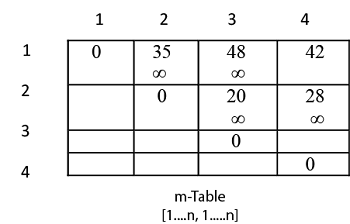
4 3 Matrix Chain Multiplication Dynamic Programming Youtube
Matrix Chain Multiplication Ppt Download
Matrix Chain Multiplication Geeksforgeeks Youtube
Matrix Chain Multiplication Ppt Download
Matrix Chain Multiplication Dp 8 Tutorialspoint Dev
Chain Matrix Multiplication
Dynamic Programming
Chain Matrix Multiplication
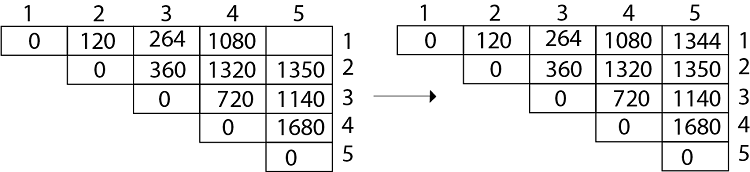
Matrix Chain Multiplication Algorithm Javatpoint
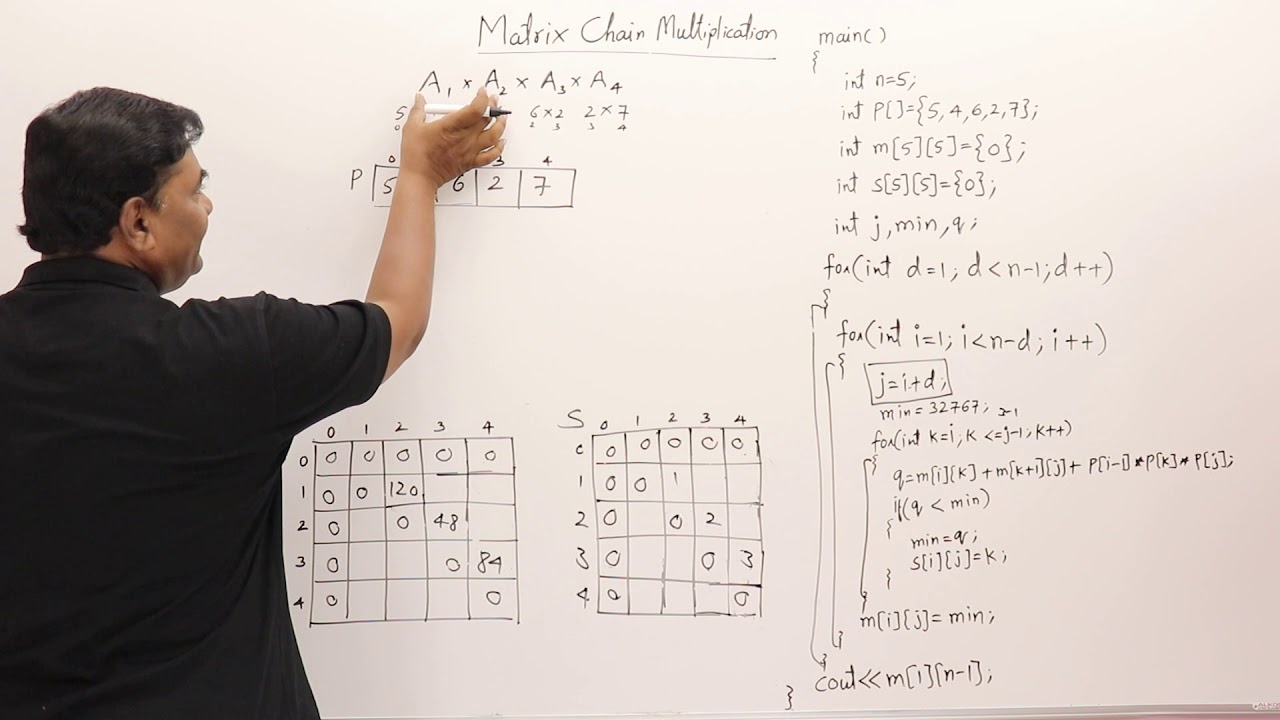
4 3 Matrix Chain Multiplication Dynamic Programming Youtube
Matrix Chain Multiplication Ordering Procedure The Mcmo Complexity Is Download Scientific Diagram
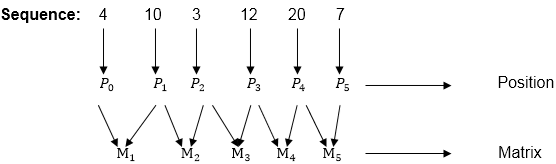
Matrix Chain Multiplication Using Dynamic Programming By Chetan More Medium
Matrix Chain Multiplication
What Are The Real World Examples Of Matrix Chain Multiplication Quora
Matrix Chain Multiplication Algorithm Javatpoint
Unit 5 Dynamic Programming Ppt Download
Matrix Chain Multiplication Ppt Download
Matrix Chain Multiplication
