Matrix Nonsingular Full Rank
It follows that the matrix A is nonsingular. A square matrix M2Rn nis called positive semide nite if xMx 0 for all x 2Rn.

Prove That If A Is Nonsingular Matrix And Ab 0 Then B Is Null Matrix Proof Youtube
Linear combinations of the columns of A so that rankAB rankA.

Matrix nonsingular full rank. For example the matrices and both have full rank. The above also implies A has linearly independent rows and columns. M2Rn n is called positive de nite if i M is positive semide nite.
Since the multiplication of all eigenvalues is equal to the determinant of the matrix A full rank is equivalent to A nonsingular. This matrix must be invertible otherwise the result is undefined. A matrix that does not have full rank is said to be rank deficient.
A square matrix which is not nonsingular is singular. Prove that if either A or B is singular then so is C. A Show that every positive de nite matrix is nonsingular ie.
In your case the data matrix X R n p is usually tall and skinny n p so the rank of everything is the number of linearly independent columnspredictorscovariatesindependent variables. N 1 m 0 m m Wdcn 1 A BBA Cd B AB A2B. 7 Less-Than-Full-Rank Linear Models In this chapter the matrix X in the model Y Xβ 71 does not have a full column rank as was the case in Chapter 6.
Let AA astAA ast-A astA. A well-known inequality for mathrm r A given by Ky Fan and Hoffman 1 is as follows. C Show that if A is nonsingular then A is invertible.
For any m n matrix rank A nullity A n. For v 2 IRn ATAv 0 if and only if Av 0. However the matrices and are rank deficient.
Thus if A is n n then for A to be nonsingular. A Show that if A is invertible then A is nonsingular. As we will see in Chapters 7 15 and 23 finding the rank of an arbitrary matrix is somewhat complex and relies on the computation of what are termed its singular values.
Add to solve later. And ii xMx 0 only if x 0. The lower bounds for the rank of matrices play an important role in diagnosing nonsingular matrices.
If rankA n then we say A is full-rank. Hence the rank of A is 3. A non-singular matrix is a square one whose determinant is not zero.
In this ce there exists a unique matrix sach that AB BA 1 Thais matrix is called the inverse of A and is denoted by A-Force-singlar A and C propretins include A AA- AC- 4C - 4 4Cc1 4-4-40 - A-44- A BCD-. A is diagonalizable iff A has n linearly independent eigenvectors. Ask Question Asked 7 years 2 months ago.
The rank of a matrix A is equal to the order of the largest non-singular submatrix of A. The last matrix is in reduced row echelon form and has three nonzero rows. RankA rankAQ rankAQQ_1 rankA so that rankA rankAQ etc.
A matrix that is not full rank is rank deficient and the rank deficiency is the difference between its smaller dimension and the rank. Recall that the rank of a matrix is the maximum number of linearly independent rows or columns1 Since A is m n with m n we necessarily have rankA n. The nn matrix is nonsingular.
A matrix is said to have full rank if its rank is either equal to its number of columns or to its number of rows or to both. Its a property of the rank operator when its used on real matrices A. How to find out if matrix is invertible regular nonsingular full rank in Eigen.
We find the rank of the matrix A as follows. The can be trAB to BA 24 Inverse ANx matrix A has full rank or is nonsingular if there is no each that Ar0. Mathrm r Ageqsum_ i1 n frac vert a_ ii vert sum_ j1 n vert a_ ij vert.
Otherwise we say A is rank-deflcient. So A is invertible. Huang and You 2 improved the Ky Fan and Hoffmans.
If A is any matrix and P and Q are any conformable nonsingular matrices then rankPAQ rankA. A matrix is of full rank if its rank is the same as its smaller dimension. Rank A rank A rank A A rank A A.
Nnp controllability matrix has rank n full row rank. Thus a non-singular matrix is also known as a full rank matrix. When computing the inverse of a matrix in Eigen it is up to the user to check if this can be done.
Let A be any m x n matrix such that r rankA and s nullity A. M2Rn nis called nonsymmetric if M6 M. Is called full-rank if rankA minfmng.
It follows that a non-singular square matrix of n nhas a rank of n. A full rank matrix which is square is nonsingular. A 1 0 1 2 1 2 1 0 1R2 2R1 R3 R1 1 0 1 0 1 0 0 0 2 1 2R3 1 0 1 0 1 0 0 0 1R1 R3 1 0 0 0 1 0 0 0 1.
B Let A B C be n n matrices such that AB C. A matrix A is nonsingular if and only if A is invertible.

Singular Matrix And Non Singular Matrix Don T Memorise Youtube

Solved You Are Given The Following Information V Is An I Chegg Com
Solved Determine If Any Of The Following Matrices Is Sing Chegg Com

4 Test Whether The Following Matrices Are Chegg Com

For A Non Singular Matrix A Of Order N The Rank Of A Is A Less Than N B Equal To N C Youtube
Solved I Find All A E R For Which The Matrix Aaa Is Inve Chegg Com

Determine Whether The Given 3 By 3 Matrices Are Nonsingular Problems In Mathematics
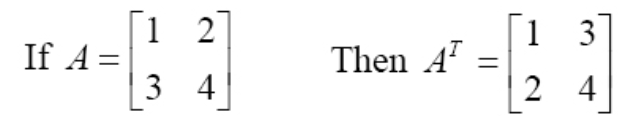
2 X 2 Invertible Matrix Studypug

How To Prove A Matrix Is Nonsingular In 10 Seconds Problems In Mathematics

14 Non Singular Matrix P And Q Such That P And Q Is Normal Form Find Non Singular Matrix Paq Youtube

Linear Algebra Ch 2 Determinants 23 Of 48 Non Invertible Matrix Example Youtube

Ex Determine If A 3x3 Matrix Is Invertible Nonsingular Using A Determinant Youtube

Singular Matrix Video Lessons Examples And Solutions

Characterizations Of Invertible Matrices Ppt Video Online Download

Invertible Matrix Theorem Youtube

Nonsingular Matrix An Overview Sciencedirect Topics

What Is A Nonsingular Matrix Quora
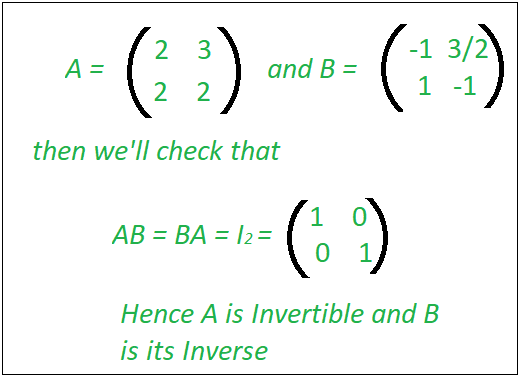
Check If A Matrix Is Invertible Geeksforgeeks

Linear Algebra Lecture 25 The Invertible Matrix Theorem Youtube

