Matrix A B C D Inverse

For two nonzero numbers a and b the sum a C b might or might not be invertible. B x B A 1 y B A 1 B x.

Gaussian Beam Propagation Code Abcd Matrices Beam Propagation

In the case of a 22 matrix A a b c d.

Matrix a b c d inverse. Let A be any n x n matrix for which det A 0. Inverse of a Matrix Formula. Matrix transpose AT 15 33 52 21 A 1352 532 1 Example Transpose operation can be viewed as flipping entries about the diagonal.

The matrix B on the RHS is the inverse of matrix A. In words to nd the inverse of a 2 2 matrix 1 exchange the entries on the major diagonal 2 negate the entries on the mi-nor diagonal and 3 divide all four entries by the determinant. There are two cases depending on whether a 0 or not.

Case a 6 0 We multiply row 1 by 1 a to get. Theorem 1 The 2 2 matrix A a b c d is invertible if and only if 6 0 where we write ad bc. I am really confused how to work with inverse matrices.

Where a b c and d represents the number. The system has at least one solution namely. Thus we have only three possible partitions.

Then A is singular not invertible. But the product ab D 9 does have an inverse which is 1 3 times 1 3. Its easy to verify that 1 actually is the inverse of A just multiply them together to get the identity matrix I.

Let Abeginbmatrix a b c d endbmatrix be the 2 x 2 matrix. That is if I is the n x n identity matrix then BA I. X 1 1 d e t X d b c a displaystyle X - 1frac 1 text det left Xright left begin matrix d- b- c aend matrixright X 1 detX1.

For 2 2 matrices there is an easy answer. To find the inverse of A using column operations write A IA and apply column operations sequentially till I AB is obtained where B is the inverse matrix of A. Or B x I B A 1 1 B A 1 y.

2 by 2 Inverse. 2 Then A x y B x so x A 1 y A 1 B x. Theorem 82 Let A a b c d.

Now Hence c d. Moreover if y is any other solution then. A b c d 1 1 ad bc d b c a.

We leave it to the reader to verify that AA 1 A 1A I. Finding the inverse of a matrix is a long and tedious process. By the product formula for determinants we have det A 1 det B 0.

We assume one of the blocks A B C or D is a nonsingular square matrix to avoid generalized inverses. K m and I -- n. The steps are.

Since the inverse of an elementary matrix is an elementary matrix A is a product of elementary matrices. Swap the positions of a and d put negatives in front of b and c and divide everything by the determinant ad-bc. 1 ad -bc d -b -c a.

Their sum aCb D 0 has no inverse. To find the inverse of a 2x2 matrix. A simple formula exists to find its inverse.

Definition The transpose of an m x n matrix A is the n x m matrix AT obtained by interchanging rows and columns of A Definition A square matrix A is symmetric if AT A. Ie AT ij A ji ij. The inverse matrix of A is given by the formula.

I have to show how this matrix is an inverse of A. In general the inverse of the 22 matrix. 2 2 matrix A a b c d Its inverse is the matrix A 1 d b c a where is the determinant of A namely ad bc.

Then A1 1 adbc d b c a. Sometimes there is no inverse at all. Note that the quantity ad bc is the determinant of A.

Then A is invertible if ad bc 6 0. Provided is not 0. 1 Start with A B x y.

It is hard to say much about the invertibility of A C B. The test for n pivots is usually decided before the determinant appears. In this case A 1 1 ad bc d b c a Proof.

If A a b c d. Write A as a product of elementary matrices. Note 6 A diagonal matrix has an inverse provided no diagonal entries are zero.

It is noted that in order to find the matrix inverse the square matrix should be non-singular whose determinant value does not equal to zero. In the next sections we will develop a technique to do so. We give it as a theorem.

Cd -C a 9 1 2 6 Set up the correct augmented matrix needed in order to find the inverse by row-reduction. Inverse of a Matrixpdf from MATH 2B at Foothill College. Square diagonal partition.

Furthermore 1 adbc is not defined when ad bc 0 since it is never possible to divide by zero. The determinant of the matrix A is written as ad-bc where the value is not equal to zero. Inverse of a Matrix we are talking about Amin x x I find i i c x Al i In 1A In Let Anxn matrix suppose B Cnxn satisfying AB BA In Ac.

It is for this reason that the inverse of A does not exist if the determinant of A is zero. Which is equivalent to. A a b c d I know that the inverse is supposed to be.

The numbers a D 3 and b D 3 have inverses 1 3 and 1 3. For two matrices A and B the situation is similar. A method for nding inverse matrices.

- 1 a b d - b Use row-reduction to compute the inverse of the matrix below if it exists and confirm your answer by comparison with the formula 1 ad-bc if ad-bc70. 3 This number adbc is the determinant of A. I B A 1 B x B A 1 y.

In this section we shall write down the formulae for E F G and H in terms of A B C and D. 3 Multiply x in step 2 by B to get. Suppose A is not singular and let B denote the inverse of A.

Suppose A is invertible. When 6 0 the inverse is A 1 1 d b c a Proof We row reduce the 2 4 partitioned matrix AjI a b 1 0 c d 0 1 2 to obtain the reduced row echelon matrix IjA 1. 9 1 2 6 Type integers or simplified fractions Find the inverse of the given matrix if it exists.

A matrix is invertible if its determinant is not zero Chapter 5.

Network Parameters Impedance And Admittance Matrices For N

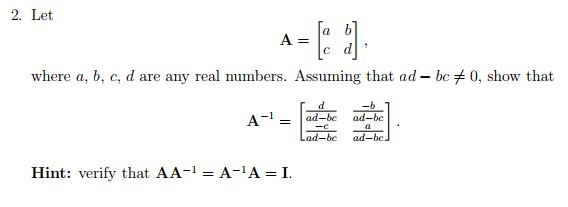
Let A A B C D Where A Is A 2x2 Matrix Where Chegg Com

If A Is The 2 2 Matrix Given By A A B C D And If Chegg Com

Gaussian Beam Propagation Code Abcd Matrices Beam Propagation

The Abcd Matrix Of Single Transmission Line And Parallel Coupled Lines Download Scientific Diagram

What Is The Ray Matrix Or Abcd Matrix For An Image Located At Infinity Physics Stack Exchange

Lesson 12 4 Inverses Of Matrices Ppt Download

Pin On 10 Math Problems

Pin On Vectors

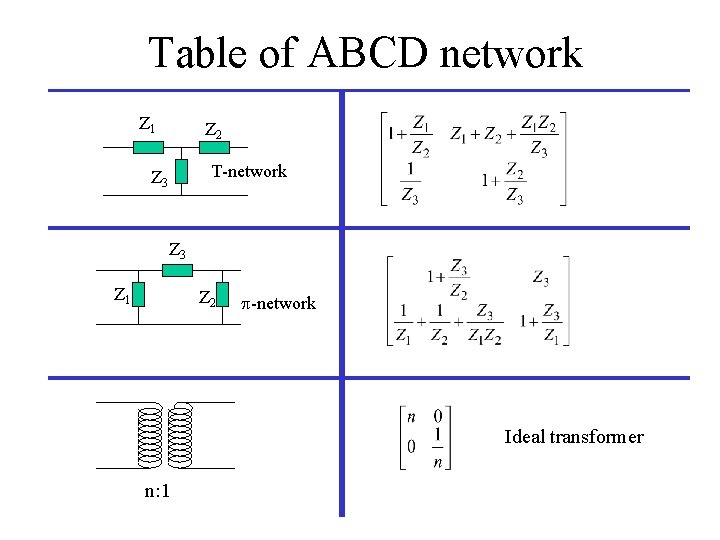
Network Parameters Impedance And Admittance Matrices For N

Solved Verify That For A 2 Times 2 Matrix A A B C D T Chegg Com

Pin On Geometry Theorems And Problems Math

How To Find New Abcd Parameters When Reversing 2 Port Network Electrical Engineering Stack Exchange

Identity Matrix Inverse Invertible Singular Matrix Determinant Multiply

3 5 Solution By Determinants The Determinant Of A Matrix The Determinant Of A Matrix A Is Denoted By A Determinants Exist Only For Square Matrices Ppt Download

Given Matrix A A B C D Prove That If Ad Chegg Com

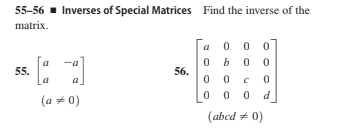
Answered 55 56 1 Inverses Of Special Matrices Bartleby

Formula For 2x2 Inverse Video Khan Academy

It Is Stated That The Inverse A 1 Of A Matrix A A Chegg Com