Matrix Multiplication Fast Algorithm
J 0 k 0g for ii0jj0kk02f1ng. The most well known fast algorithm is due to Strassen andfollows the same block structure.
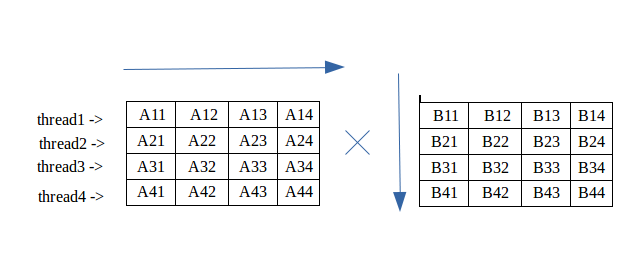
Multiplication Of Matrix Using Threads Geeksforgeeks
Which means that at n2000 your algorithm requires 100 times as much computation as the best algorithm.

Matrix multiplication fast algorithm. Strassens algo-rithm is an improvement over the naive algorithm in the case of multiplying two 22 matrices. K for int j 0. SIAM News Nov 2005 by Sara Robinson.
B2RnnandCABwherenis a power of two2We writeAandBas block matrices. As It can multiply two n n matrices in 0 n2375477 time. Notice that the Fourier matrix is a unitary matrixthat is FnF I therefore the conjugate transposeF.
Idea - Block Matrix MultiplicationThe idea behind Strassens algorithm is in the formulationof matrix multiplication as a recursive problem. 1 check that the dimensions agree eg. J swapped order cij aik bkj.
Nn denote the number of arithmetic operations that the above algorithm needs to multiply polynomial of degree n. Group-theoretic algorithms for matrix multiplication FOCS Proceedings 2005. Since matrix multiplication is asymptotically moreexpensive than matrix addition this tradeoresults in faster algo-rithms.
Algorithms and implementation a dissertation submitted to the department of electrical engineering and the committee on graduate studies of stanford university in partial fulfillment of the requirements for the degree of doctor of philosophy by gary w. When doing matrix multiplying you use naive multiplication method which takes time of O n3. Similarly to the analysis of Strassens algorithm.
We want to multiply them as fast as possible. For int i 0. 3x3 3x1 and not 3x3 1x3 2 multiply the corresponding fields together and add to arrive at the final field.
I have tried to look at the original paper and it scares me. Notation The tensor is often notated as hnmpi. Found groups with subsets beating the sum of the cubes and satisfying the triple product property.
Viewed 868 times -2 Recently I have learned about both the Strassen algorithm and the CoppersmithWinograd algorithm independently according to the material Ive used the latter is the asymptotically fastest known matrix multiplication algorithm until 2010. Chinmay Nirkhe Fast Matrix Multiplication. The algorithm above gives the following recursive equation Nn3Nn12 1On and N27.
For xed n the matrix multiplication tensor T 2Cnm mp pn de ned by T ij0jk 0ki 1 f i 0. According to wikipedia there is an algorithm of Coppersmith and Winograd that can do it in O n 2376 time. Matrix mult_stdmatrix a matrix b matrix cadim false false.
2 Randomized Linear Algebra Algorithms Goal. The idea of fast matrix multiplication algorithms is to performfewer recursive matrix multiplications at the expense of more ma-trix additions. I for int k 0.
To develop and analyze fast Monte Carlo algorithms for performing useful computationson large matrices. We rst cover a variant of the naive algorithmformulated in terms of block matrices and then parallelize it. Fast and stable matrix multiplication p1344.
Matrix Multiplication Computation of the Singular Value Decomposition. Matrix multiplication is fairly simple. Fast matrix multiplication is still an open problem but implementation of existing algorithms 5 is a more com-mon area of development than the design of new algorithms 6.
There exist matrix multiplication algorithm which takes O n24. It is well known that the product of this matrix with any vector is the so-calleddiscrete Fourier transform which can be done efficiently using the fast Fourier trans-form FFT algorithm Cooley65. Suppose we have two n by n matrices over particular ring.

Sparse Matrix Multiplication Description By Glyn Liu Medium

Matrix And Matrix Multiplication C Youtube Matrix Multiplication Multiplication Matrix
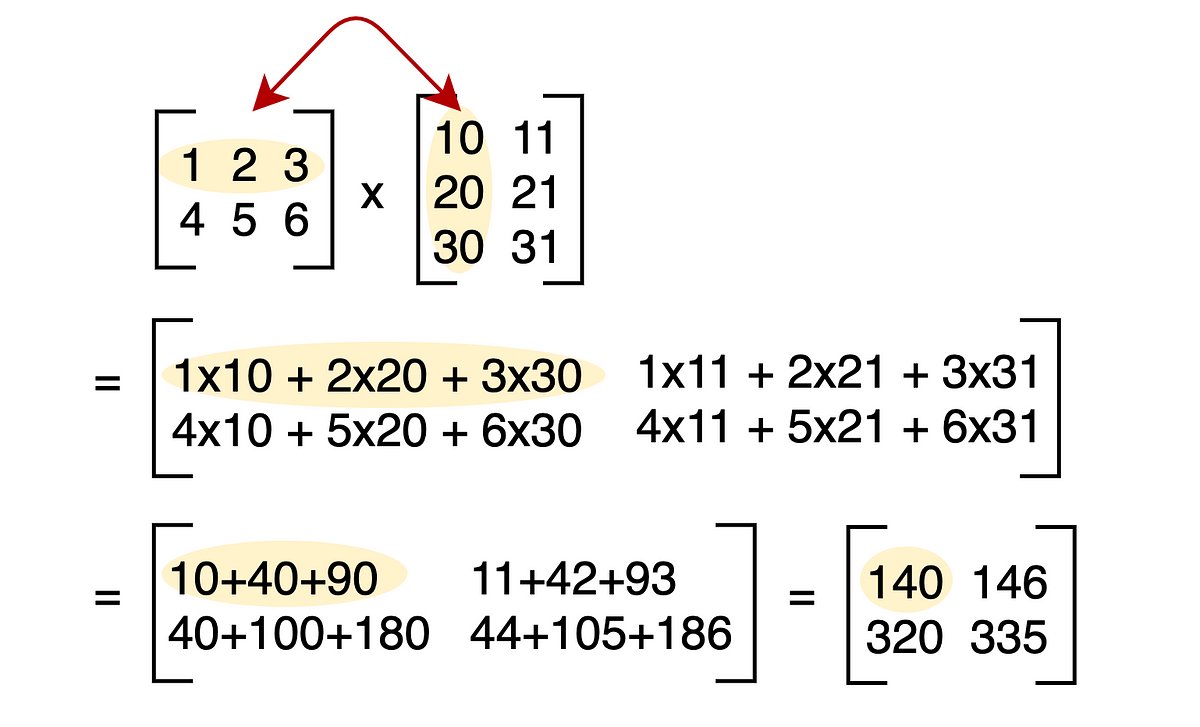
A Complete Beginners Guide To Matrix Multiplication For Data Science With Python Numpy By Chris The Data Guy Towards Data Science
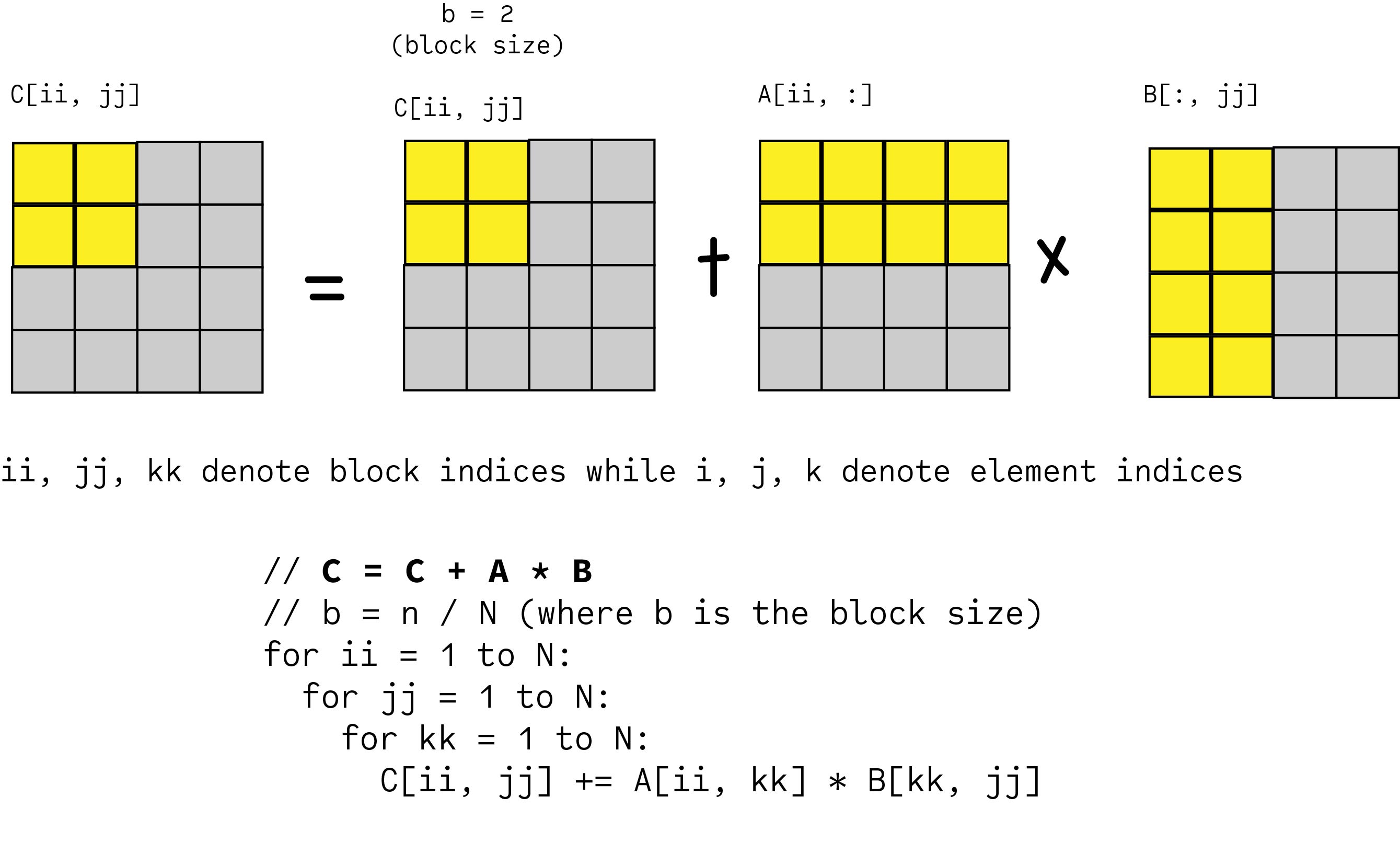
Blocked Matrix Multiplication Malith Jayaweera

Performing Convolution By Matrix Multiplication F Is Set To 3 In This Download Scientific Diagram
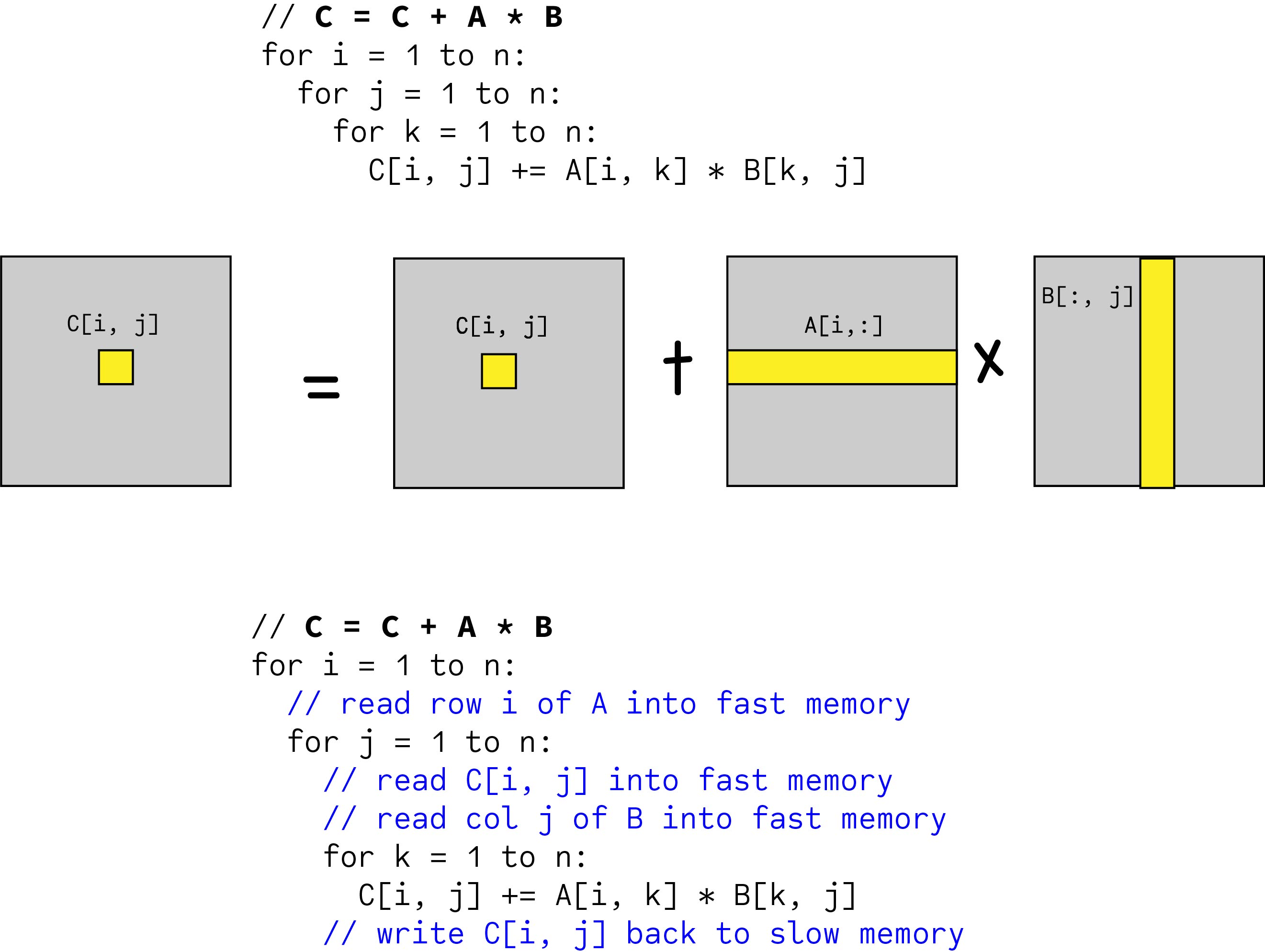
Blocked Matrix Multiplication Malith Jayaweera

Communication Costs Of Strassen S Matrix Multiplication February 2014 Communications Of The Acm
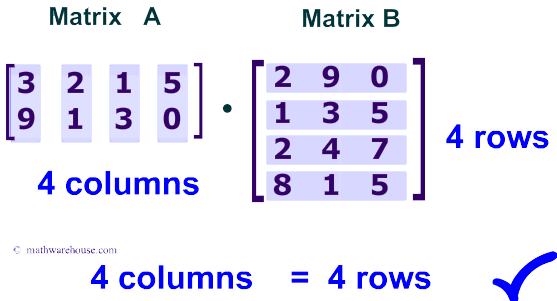
Matrix Multiplication In C Applying Transformations To Images Codeproject

Matrix Multiplication With 1 Mapreduce Step Geeksforgeeks

An Intuitive Guide To Linear Algebra Betterexplained Algebra Matrix Multiplication Linear

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
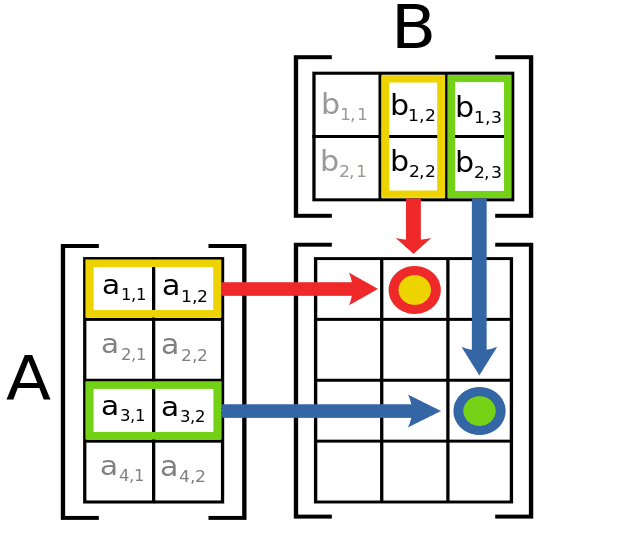
Introduction To Matrices And Matrix Arithmetic For Machine Learning

Matrix Element Row Column Order Of Matrix Determinant Types Of Matrices Ad Joint Transpose Of Matrix Cbse Math 12th Product Of Matrix Math Multiplication
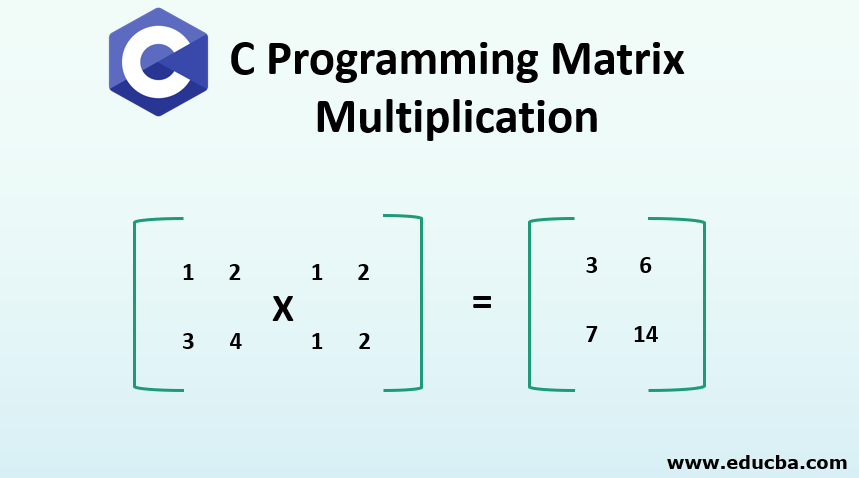
C Programming Matrix Multiplication C Program For Matrix Manipulation

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov



