Time Complexity Of Matrix Multiplication Algorithm
In particular for 1 i p and 1 j. Firstly the time complexity of the algorithm is O n 3 which is too high.

Numerical Algorithms Matrix Multiplication Ppt Download
It was the first algorithm to prove that the basic O n3 runtime was not optiomal.

Time complexity of matrix multiplication algorithm. Since then we have come a long way to better and clever matrix multiplication algorithms. The fastest known matrix multiplication algorithm is Coppersmith-Winograd algorithm with a complexity of On 23737. We can decompose matrix into LUP decomposition but we still dont get product of two lower or upper triangular matrices endgroup Pranav Bisht Mar 31 20 at 1745.
That is you can multiply two matrices if they are compatible. Ignore minor details such as the house keeping aspects of the algorithm. Strassens algorithm Weve all learned the naive way to perform matrix multiplies in On3 time1 In todays lecture we review Strassens sequential algorithm for matrix multiplication which requires Onlog 2 7 On281 operations.
Solvay Strassen algorithm achieves a complexity of On 2807 by reducing the number of multiplications required for each 2x2 sub-matrix from 8 to 7. The time complexity is ON 28074. T N 7T N2 O N 2 From Masters Theorem time complexity of above method is O N Log7 which is approximately O N 28074 Generally Strassens Method is not preferred for practical applications for following reasons.
So time complexity can be written as. Volker Strassen first published his algorithm in 1969. The Algorithm multiplied by the Strassen matrix is compared to a normal algorithm but only one multiplication there are many time complexity.
In general multipling two matrices of size N X N takes N3 operations. Secondly the multiplication of more than two matrices will not only increase the confusion and complexity of the program but also increase the time complexity accordingly. You can multiply a matrix A of p q dimensions times a matrix B of dimensions q r and the result will be a matrix C with dimensions p r.
Addition and Subtraction of two matrices takes O N 2 time. MATHPOWER M n if n 1 then return M else P MATHPOWER M floorn2 if n mod 2 0 then return P P else return P P M Share. It can be seen that a small difference may lead to a big difference.
The best known algorithm has complexity approximately On23728639. Here is the best video for time complexity of design and analysis of algorithmstimecomplexity strassens matrix multiplication DAA design analysis al. If all three matrices were square then the fastest known algorithm for multiplying two of them has complexity O N 23729.
Note that the operator denotes ordinary matrix multiplication. There are three for loops in. Here we assume that integer operations take O1 time.
Provides an upper bound. This means that multiplying three N N matrices will have complexity just under O N 475. Following is the algorithm.
The naive algorithm has complexity Omjn for multiplying an m x j matrix by a j x n matrix or On3 for square n x n matrices. Matrix-Multiplication X Y Z for i 1 to p do for j 1 to r do Zij 0 for k 1 to q do Zij Zij Xik Ykj Complexity. Enjoy the videos and music you love upload original content and share it all with friends family and the world on YouTube.
See the wikipedia article on matrix multiplication. Running The following is the implementation process. More difficult to determine the average case time complexity of an algorithm average.
Unless the matrix is huge these algorithms do not result in a vast difference in computation time. However it is unknown what the underlying complexity actually is. Enter the 4 elements of first matrix.
Operations addition multiplication etc. The number of columns of A must equal the number of rows of B. Begingroup I also dont see any easy way to reduce general matrix multiplication to lower triangular multiplication.
5 6 1 7 Enter the 4 element of second matrix. Focus on the worst-case time complexity of an algorithm. Browse other questions tagged algorithms time-complexity matrices or ask your own question.
As before if we have n matrices to multiply it will take O n time to generate each of the O n2 costs and entries in the best matrix for an overall complexity of O n3 time at a cost of O n2 space. 6 2 8 7 The first matrix is 5 6 1 7 The second matrix is 6 2 8 7 After multiplication 78 52 62 51 Complexity.

Time Complexity Of Clrs Optimal Parenthesis Algorithm Mathematics Stack Exchange

Strassen S Matrix Multiplication Algorithm When N Is Not A Power Of 2 Computer Science Stack Exchange

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Strassen S Matrix Multiplication Divide And Conquer Geeksforgeeks Youtube

Computational Complexity Of Matrix Vector Product Mathematics Stack Exchange
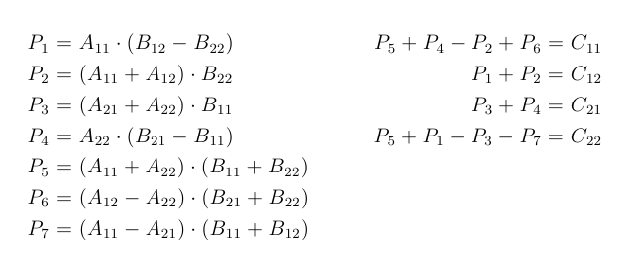
Strassen Matrix Multiplication C The Startup
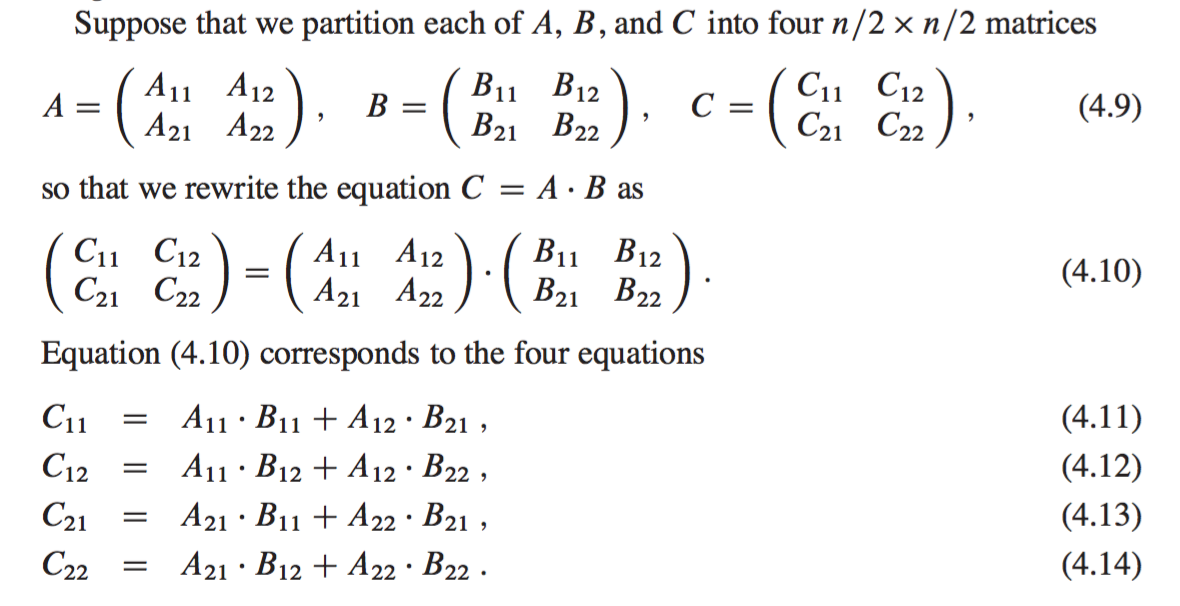
Matrix Multiplication Using The Divide And Conquer Paradigm
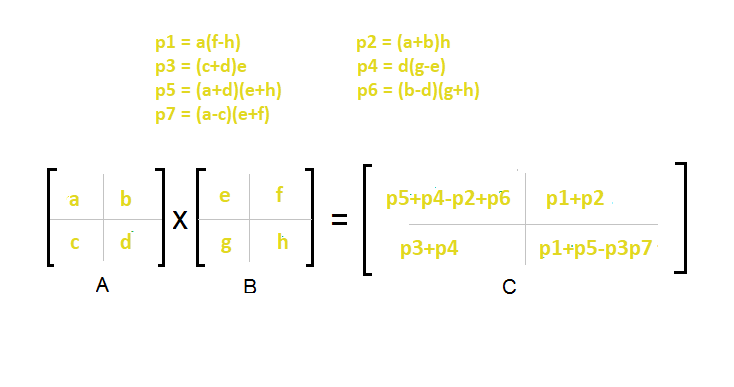
Strassen S Matrix Multiplication Algorithm
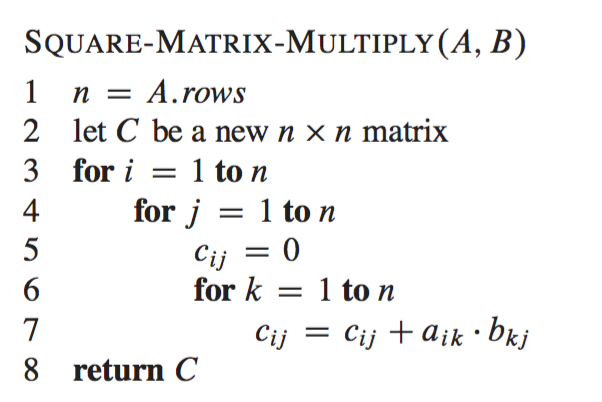
Matrix Multiplication Using The Divide And Conquer Paradigm

Communication Costs Of Strassen S Matrix Multiplication February 2014 Communications Of The Acm

Time Complexity Of Matrix Multiplication In Big Align Computer Science Stack Exchange

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
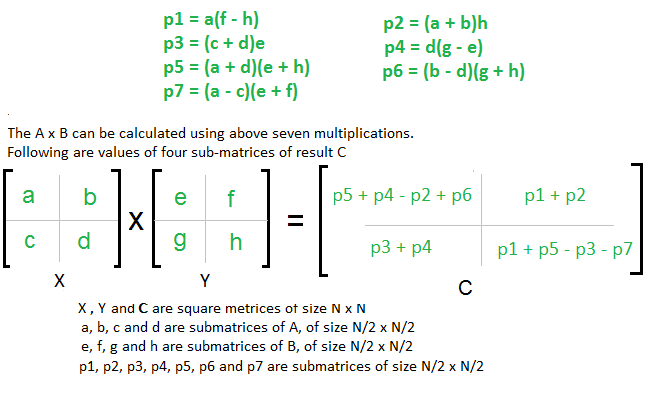
Easy Way To Remember Strassen S Matrix Equation Geeksforgeeks

2 9 Strassens Matrix Multiplication Youtube

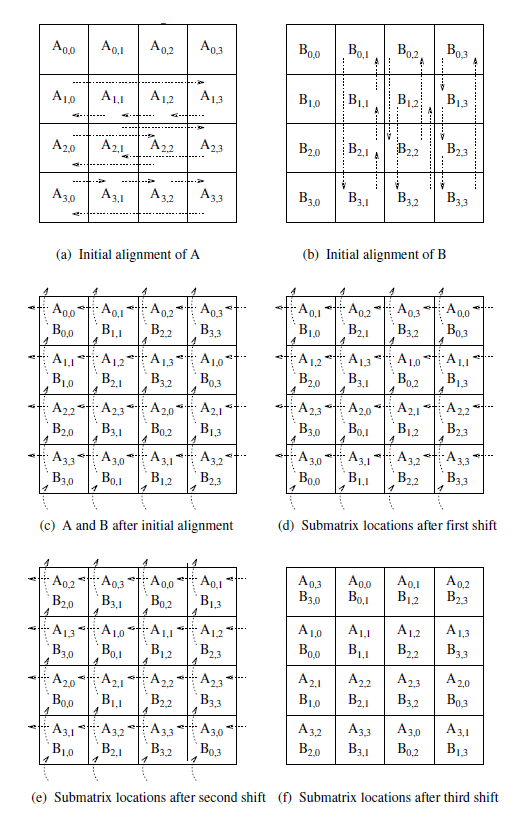
Systolic Arrays Algorithm For Matrix Multiplication Mathematics Stack Exchange

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
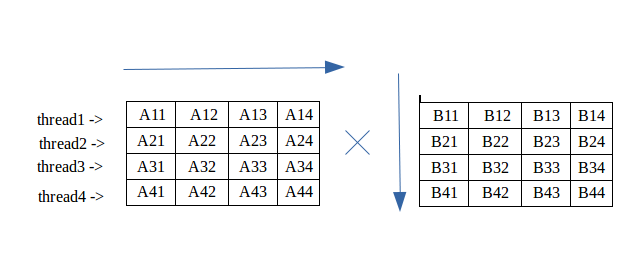
Multiplication Of Matrix Using Threads Geeksforgeeks
Cannon S Algorithm For Distributed Matrix Multiplication

Time Complexity Of Strassen S Matrix Multiplication In Daa Design And Analysis Of Algorithms Youtube