Matrix Invertible Proof
The columns of A span R n. B Let A B C be n n matrices such that AB.

If A Is An Invertible Matrix Then Prove That A 1 A 1 Maths Matrices 10925735 Meritnation Com
A matrix A is invertible if and only if there exist A 1 such that.

Matrix invertible proof. Let A 1nxn. Then multiplying both sides of this equationon the right byP1weobtainPAP1 Bor P11AP1 B. The n x n matrix consisting of all ones.
2 We say that A is invertible if A is both left. A Show that if A is invertible then A is nonsingular. A 1 A 4 I 7.
If you had the value of A you would only calculate its determinant and check if it is non zero. Suppose BA D I and also AC D I. By definition of inverse matrices if there is an n n matrix B such that A T B I and B A T I where I is the n n identity matrix then A T is invertible and its.
In linear algebra an n -by- n square matrix A is called invertible also nonsingular or nondegenerate if there exists an n -by- n square matrix B such that where In denotes the n -by- n identity matrix and the multiplication used is ordinary matrix multiplication. Namely A is nilpotent if there exists a positive integer k such that A k O where O is the zero matrix. Suppose that A is a nilpotent matrix and let B be an invertible matrix of the same size as A.
If Ais invertible andc 0is a scalar thencAis invertible andcA11cA1. So A 1 exists hence A is invertible. If Ais invertible thenA1is itself invertible andA11A.
We call D a right inverse of A. A square matrix A is called nilpotent if some power of A is the zero matrix. Therefore the system of equations A x 0 has no non-trivial solution and so A is invertible.
A square matrix is invertible if and only if its determinant is non-zero. A A 1 I. Thisshows thatBQ1AQwhereQis the matrixQP1 which is invertibleThus Bis similar toA.
Then B D C according to this proof by parentheses. TheoremProperties of matrix inverse. The columns of A are linearly independent.
Say that A is right invertible if there exists an n m matrix D such that AD I m. Find a formula for A r 1. The one most people consider is showing that the determinant of the matrix is not equal to zero.
Is the matrix B A invertible. The proof of Theorem 2. BACD BAC gives BI D IC or B D C.
Suppose that A is an invertible matrixThen since the equation Ax b has a solution for each b A has a pivot position in every rowBecause A is square the n pivot positions must be on the diagonal which implies that the reduced echelon form of A is In. Suppose A is an nxn matrix satifying PA Onxn a. Recall the three types of elementary row operations on a matrix.
Find the determinant of matrix E. Suppose further that A is not a scalar multiple of In. Justify your answer using a proof by induction.
Lets prove that there exists a Right Inverse. So from our previous answer we conclude that. 2 This shows that a left-inverse B multiplying from the left and a right-inverse C multi-plying A from the right to give AC D I must be the same matrix.
Let A be an n n matrix and let T. We know CAB Multiplying B-1 from right on both sides CB-1 ABB-1 CB-1 AI CB-1 A Multiplying both sides by A-1 from right CB-1A-1 AA-1 CB-1A-1 I This proves that the Right InverseD for C is B-1A-1. Det A 0 A is invertible.
If c 0 Question. Invertible Matrix Theorem You can prove the matix is invertible by showing that any of those properties hold. Note 2 The matrix A cannot have two different inverses.
R n R n be the matrix transformation T x Ax. The inverse of a matrixAis uniqueand we denote itA1. The following statements are equivalent.
Use the multiplicative property of determinants Theorem 1 to give a one line proof that if A is invertible then detA 6 0. Reorganize the entries of matrix E to conform with the formula and substitute the solved value of the. If Ais similar toB then there exists an invertiblenxnmatrixP such thatAP1BP.
If an n n symmetric A is positive definite then all of its eigenvalues are positive so 0 is not an eigenvalue of A. If c 0 then A is invertible. Ax b has a unique solution for each b in R n.
I dont get how knowing that 0 is not an eigenvalue of A enables us to conclude that A x 0 has the trivial solution only. Verify your answer by checking that you get the Identity matrix in both scenarios. Multiplying both sides ofthisequationontheleftbyPweobtainPABP.
A has n pivots. A matrix A is nonsingular if and only if A is invertible.

Example Proving That The Left Inverse Of A Matrix Is The Same As The Right Inverse Youtube

Properties Of The Inverse Matrix

Why Is A Matrix Invertible If It Can Be Written As The Product Of Elementary Matrices Mathematics Stack Exchange

Ex Determine If A 3x3 Matrix Is Invertible Nonsingular Using A Determinant Youtube

Invertible Matrix Theorem Youtube

Why Can All Invertible Matrices Be Row Reduced To The Identity Matrix Mathematics Stack Exchange
Invertible Matrix Theorems Math 343 Linear Algebra Section 2
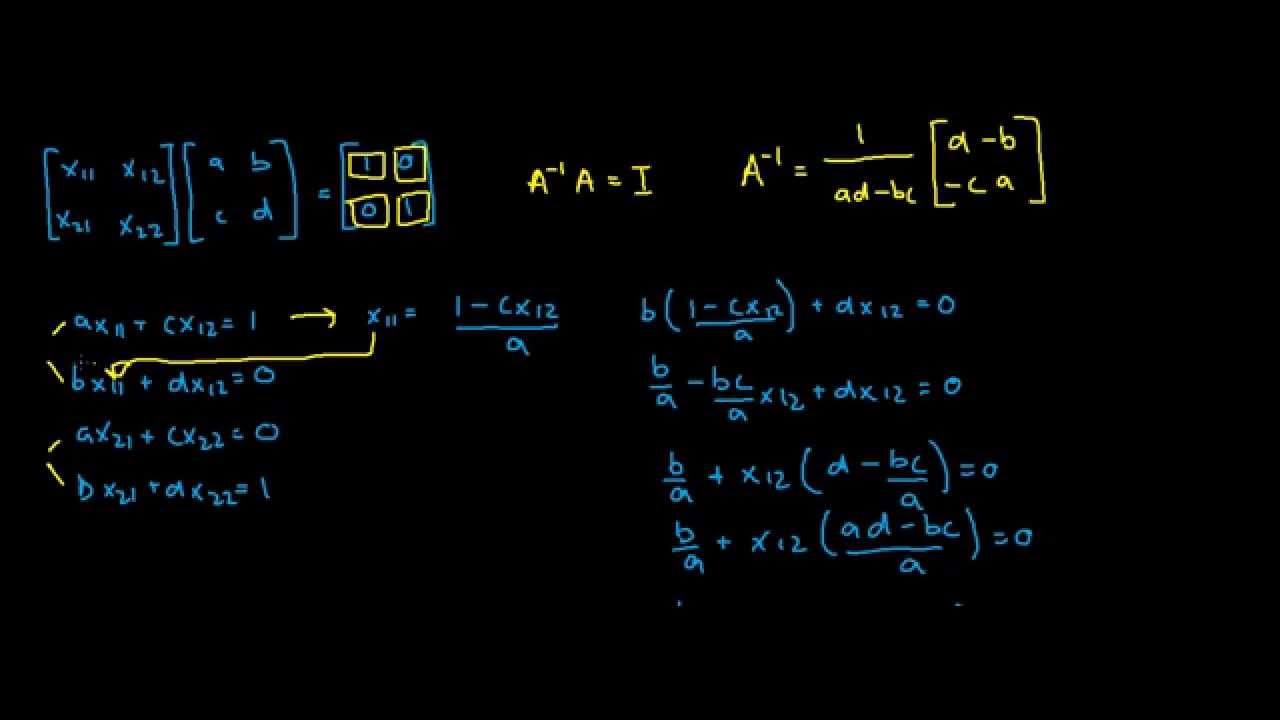
Proof Of 2x2 Matrix Inverse Formula Youtube

Linear Algebra Lecture 25 The Invertible Matrix Theorem Youtube
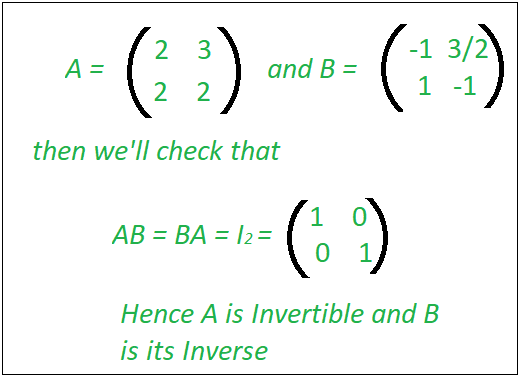
Check If A Matrix Is Invertible Geeksforgeeks

Determinant Method For Inverse Matrices Proof Youtube

Matrix Inverse Properties Youtube

4 Proofs Prove The Following A If A Is An Chegg Com

Linear Algebra 85 Inverse Of A Matrix Proof Youtube

Characterizations Of Invertible Matrices Ppt Download

Characterizations Of Invertible Matrices Ppt Video Online Download

Determinant Theorems And Proofs Part 3 Of 4 Invertible Youtube

Linear Algebra Inverse Matrix Prove Youtube

Linear Algebra Characterizations Of Invertible Chegg Com