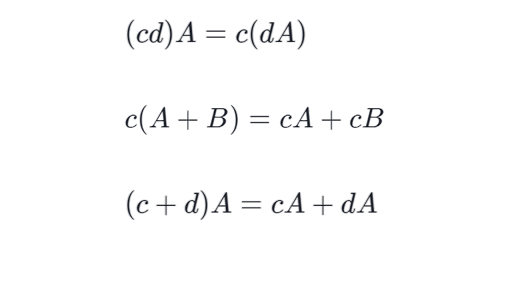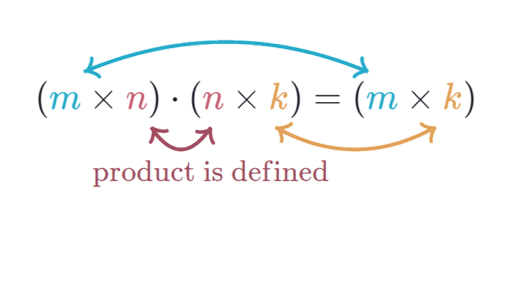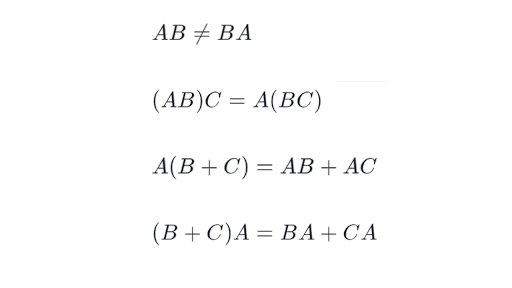Matrix Multiplication And Dot Product Relationship
First row first column. 17 The dot product of n-vectors.
Section 34 Matrix Multiplication permalink Objectives.

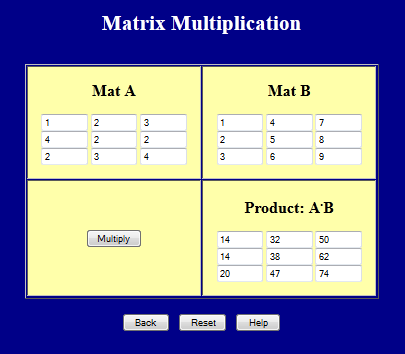
Matrix multiplication and dot product relationship. To get upper right result use row 1 A column 3 B. Matrix multiplication two ways. In other words the component in the i th row and j th column of C is the dot product between the i th row of A and the j th column of B.
The quadratic form associated to Ais the function Q A. In the special case where the matrix Ais a symmetric matrix we can also regard Aas de ning a quadratic form. A B row 1 colum1 x T y.
Matrix multiplication does not commute in other words A times B does not equal B times A in general2084. C ij p k 1a ikb kj. 1 8 2 10 3 9 55.
This gives the first row of the product. 1 2 2 1 3 3 13. Matrix multiplication presents a more significant challenge.
If you had matrix 1 with dimensions axb and matrix 2 with cxd then it depends on what order you multiply them. Matrix multiplication For m x n matrix A and n x p matrix B the matrix product AB is an m x p matrix. In math we write this component of C as c i j a i 1 b 1 j a i 2 b 2 j a i n b n j.
Understand compositions of transformations. The result of this dot product is the element of resulting matrix at position 00 ie. The inverse of a rotation matrix is its transposeWe call these matrices Orthogonal MatricesThe rotations in three dimensions are a representation of the Special Orthogonal Group SO3These matrices have determinant 1.
X n 3 5 Notice that quadratic forms are not linear transformations. To calculate the c i j entry of the matrix C A B one takes the dot product of the i th row of the matrix A with the j th column of the matrix B. Dot products and matrix multiplication.
The first step is the dot product between the first row of A and the first column of B. Multiplication of two matrices involves dot products between rows of first matrix and columns of the second matrix. U a1anand v b1bnis u 6 v a1b1 anbn regardless of whether the vectors are written as rows or columns.
Dot product of 2-D vectors. Then each column of C is the matrix-vector product of A with the respective column of B. V 1 a 1 a 2 a n v 2 b 1 b 2 b n v 1 v 2 a 1 b 1 a 2 b 2 a n b n.
A dot product takes the product of two matrices and outputs a single scalar value. 18 If A aijis an m n matrix and B bijis an n p matrix then the product of A and B is the m p matrix C cijsuch that. Matrix product is defined between two matrices.
Outer parameters become parameters of matrix AB What sizes of matrices can be multiplied together. If A and B are n n matrices the dot product of row i of A and column j of B is the sum of the product of each entry in row i from A with the corresponding entry in column j from B. Matrix Multiplication is the dot Product for matrices.
If A is an m p matrix and B is a p n matrix the product is an m n matrix whose elements are. While working with matrices there are two major forms of multiplicative operations. After that we talked about matrix multiplication where we actually invoke the dot product so with matrix multiplication you can only multiply two matrices if the number of columns in the first matches the number of rows in the second2070.
To multiply matrices they need to be in a certain order. Heres a picture of that for 2-D vectors. 1 4 2 5 3 6 32.
Q Ax xAx is the dot product xTAx x 1 x n A 2 4 x 1. Let Abe a symmetric n nmatrix. They are different operations between different objects.
Start with i 1 and apply the formula for j 1 2. Kind of like subtraction where 2-3 -1 but 3-21 it changes the answer. A i1B 1j A i2B 2j A inB nj If A and B are n n matrices over the integers then the matrix product of A and B denoted AB or AB is another n n matrix such that AB.
The process taking place in Matrix Multiplication is taking the dot product of the transpose of a row vector in Matrix A dot its corresponding column vector in Matrix B. To calculate the result sum the product of each matching pair. If we include parity inversions with rotations we have the larger Orthogonal Group O3These matrices have.
Understand the relationship between matrix products and compositions of matrix transformations. So if you did matrix 1 times matrix 2. Likewise to get the upper middle result use row 1 A column 2 B.
The two are used interchangeably. The connection between the two operations that comes to my mind is the following. Dot product is defined between two vectors.
Become comfortable doing basic algebra involving matrices. If A is a square matrix and k is a positive integer we define Ak A AA k factors Properties of matrix multiplication. Dot Product and Matrix Multiplication DEFp.
Finally the dot product can be thought of as a row vector or a 1 n matrix multiplied by a column vector an n 1 matrix. On the other hand matrix multiplication takes the product of two matrices and outputs a single matrix.

What Is The Relationship Between Matrix Multiplication And The Dot Product Quora
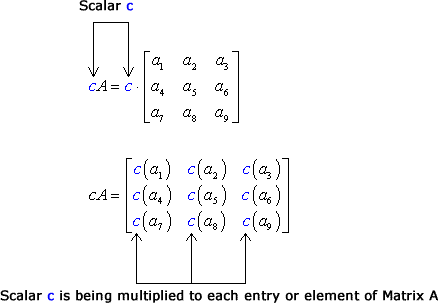
Scalar Multiplication Chilimath
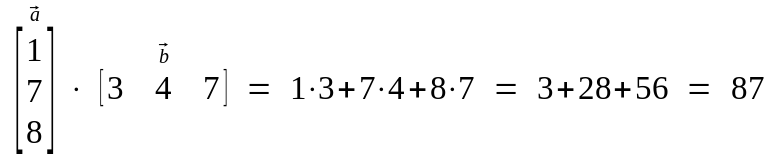
Part 14 Dot And Hadamard Product By Avnish Linear Algebra Medium

The Geometric Meaning Of Covariance In 2021 Geometric Inner Product Space Meant To Be
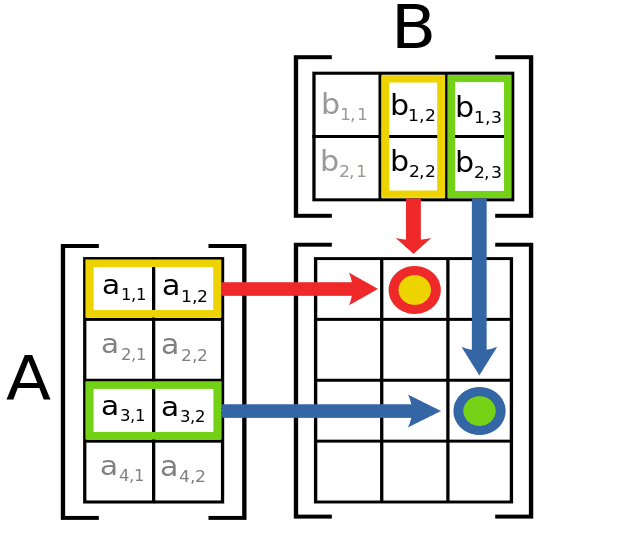
Introduction To Matrices And Matrix Arithmetic For Machine Learning

Understand Dot Products Matrix Multiplications Usage In Deep Learning In Minutes Beginner Friendly Tutorial By Uniqtech Data Science Bootcamp Medium
Properties Of Matrix Scalar Multiplication Article Khan Academy

Multiplication Of 3x3 Matrices Matrix Multiplication Youtube
Matrix Multiplication Dimensions Article Khan Academy

Cross Product Of Two Vectors Explained Youtube
Matrix Matrix Multiplication Ml Wiki
Matrix Matrix Multiplication Ml Wiki
Properties Of Matrix Multiplication Article Khan Academy

Matrix Multiplication In C Applying Transformations To Images

Pin On Matrices And Linear Systems High School Math Classroom Resources
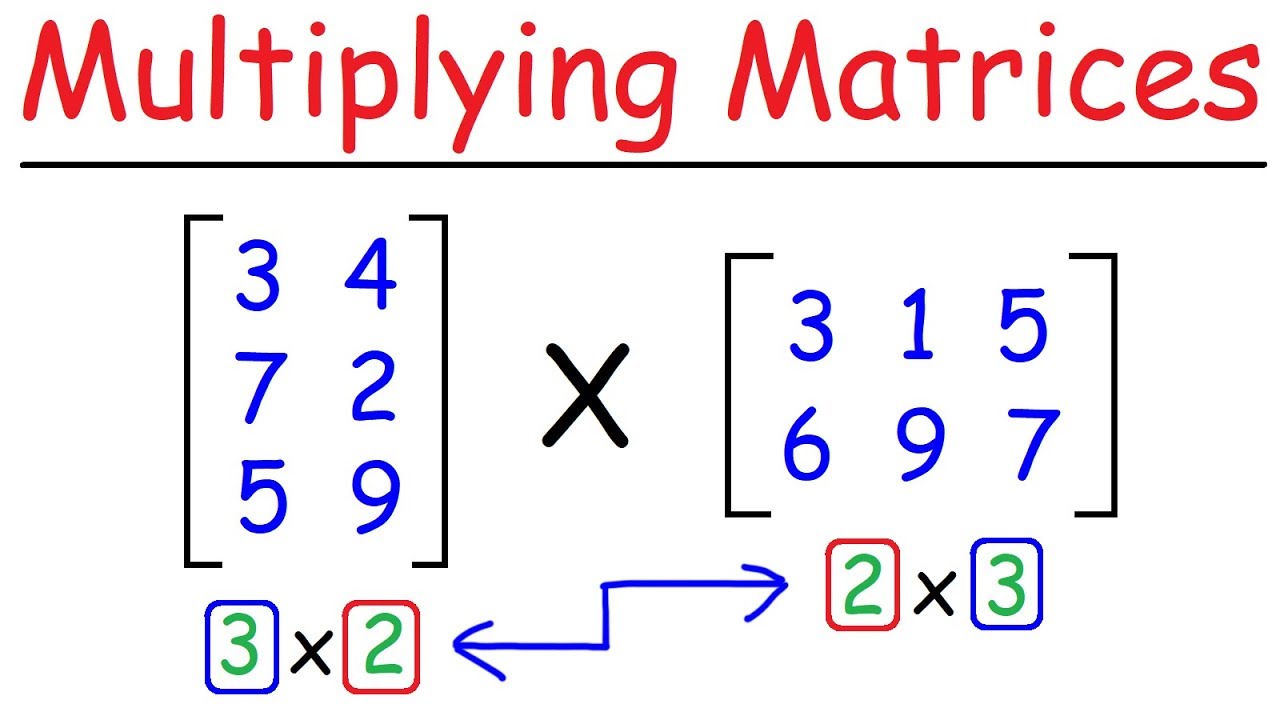
How To Multiply Matrices Quick Easy Youtube