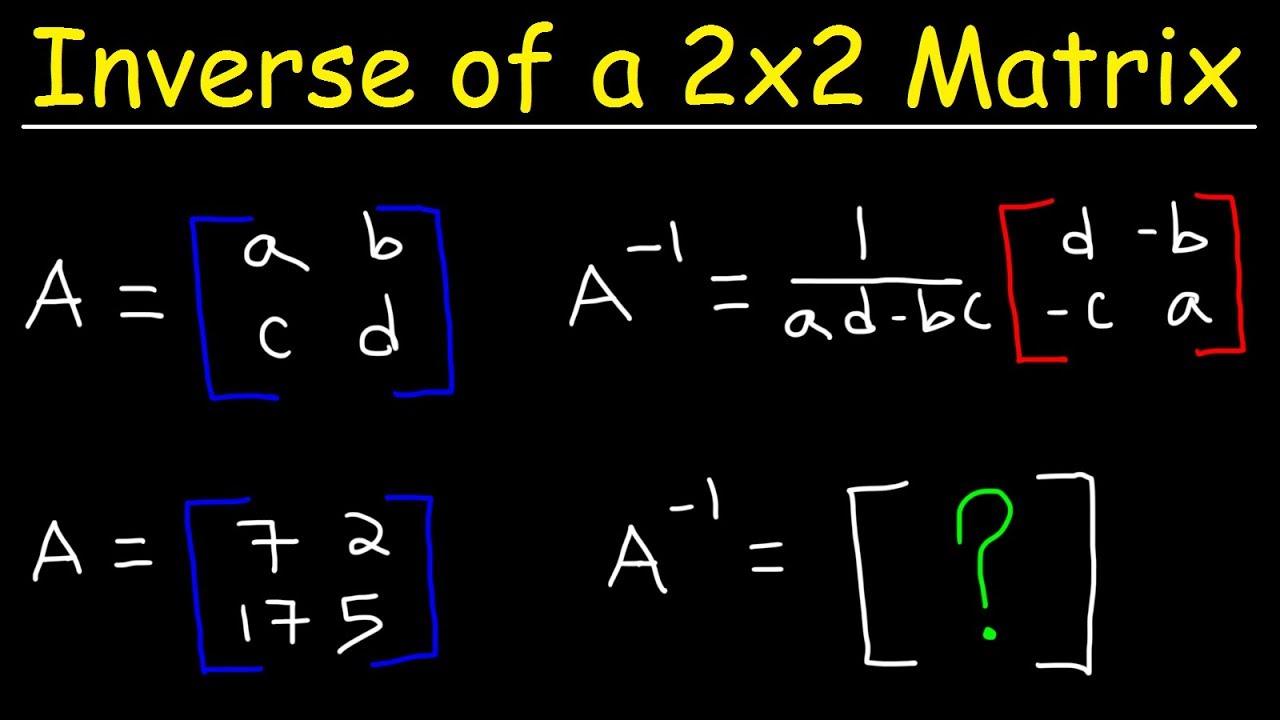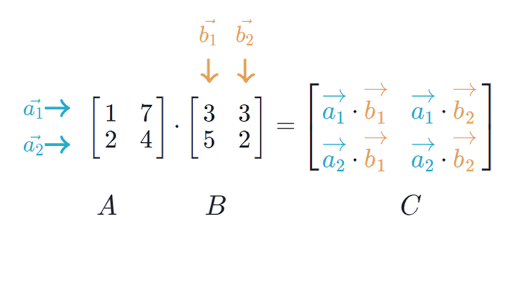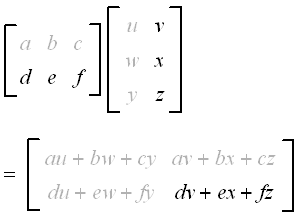When You Multiply A Matrix By The Identity Matrix You Obtain The Transpose Matrix
Try the math of a simple 2x2 times the transpose of the 2x2. To see if this is true for AB write the size of Axthe size of B in the format n x m x n x m and if the centre two numbers are equal the matrices are multiplicably conformable.

Rendering Matrix Transformations And The Graphics Pipeline Ppt Download
Transcribed Image Textfrom this Question.

When you multiply a matrix by the identity matrix you obtain the transpose matrix. If there were such a T we would have that T T times I IT I where I is the identity matrix. Transpose matrix mInverse inv m. Ie that all matrices are their own transposes.
But then it would follow that A I times A T times A AT for all matrices A. Then the user is asked to enter the elements of the matrix of order rc. In arithmetic there is one number which does not have a multiplicative inverse.
M 1 2. Definition of the inverse of a matrix. A-1A I AA-1 That is the inverse of A is the matrix A-1 that you have to multiply A by in order to obtain the identity matrix I.
Multiplying a matrix by the identity matrix I thats the capital letter eye doesnt change anything just like multiplying a number by 1 doesnt change anything. Ie AT ij A ji ij. Pull the transpose outside eliminate the brackets.
The transpose of a matrix is a new matrix that is obtained by exchanging the rows and columns. If A is a 2 x 2 matrix and A -1 is its inverse then AA -1 I 2. That is kA kA where k is a constant.
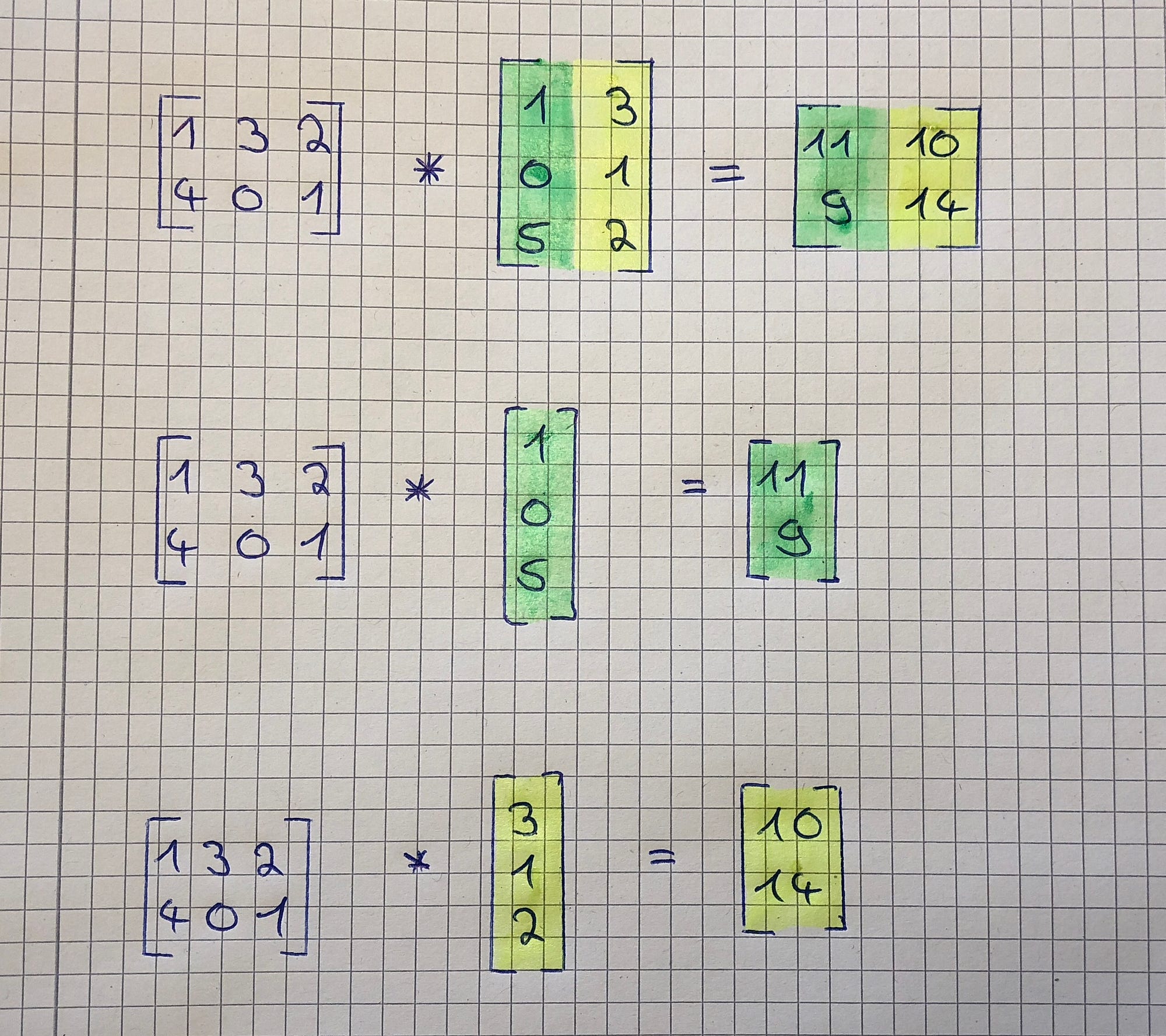
Before you can multiply two matrices together the number of ____ in the first matrix must equal the number of rows in the second matrix. Original matrix Odcofactor matrix. - the number of columns in matrix A must be equal to the number of rows in matrix B.
So thats the transpose of the normal product with the transpose of the known transformation matrix product with the transformation were solving for. When you multiply a matrix by the identity matrix you obtain the inverse matrix. Multiply matrix 5 -3 3 -2 by -4 3 -11 6 11 -6 -6 11 -11 6 none of the above.
Note that I am not just trying to be cute by including in that first sentence. Definition The transpose of an m x n matrix A is the n x m matrix AT obtained by interchanging rows and columns of A Definition A square matrix A is symmetric if AT A. Transpose Ntranspose ABV 0.
Because when you multiply them together you get the multiplicative identity one. Their values should be less than 10 in this program. Matrix transpose AT 15 33 52 21 A 1352 532 1 Example Transpose operation can be viewed as flipping entries about the diagonal.
Size m 1 number of rows size m 2 number of columns. Transpose inverse and identity matrix. In basic arithmetic when a number a is multiplied by the multiplicative identity 1 its value remains unchanged.
A related matrix formed by making the rows of the matrix into columns and the columns into rows is called columns. Viz a1a1a Analogously when a matrix A is multiplied by the identity matrix I it results in the same matrix A viz AI. When you multiply a matrix by the identity matrix you obtain the Inverse matrix The transpose matrix Adjoint method Original matrix.
As this is not. Now you can use a matrix to show the relationships between all these measurements and state variables. The outer 2 values give the matrix.
If a matrix is multiplied by a constant and its transpose is taken then the matrix obtained is equal to transpose of original matrix multiplied by that constant. The same is true of matrices. Identity square matrix nxn Extract data from a matrix.
In this program the user is asked to enter the number of rows r and columns c. When you multiply a matrix by the identity matrix you obtain the a. That is when you multiply a matrix by the identity you get the same matrix back.
The inverse A-1 of a square matrix A is the unique matrix such that. So now if we transpose the matrix and multiply it by the original matrix look at how those equations in the matrix are being multiplied with all the other variables and itself. This property of leaving things unchanged by multiplication is why I and 1 are each called the multiplicative identity the first for matrix multiplication the latter for numerical multiplication.
That number is zero because. Inverse matrix identityMatrix eye n.
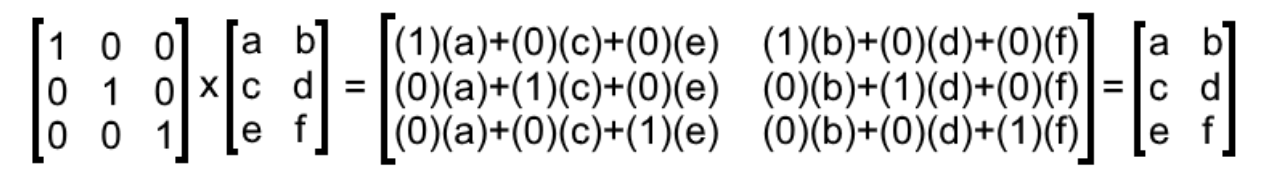
What Is An Identity Matrix Studypug
If You Multiply A 1x2 Matrix By A 2x1 Matrix What Are The Dimensions Of The Resulting Matrix Quora
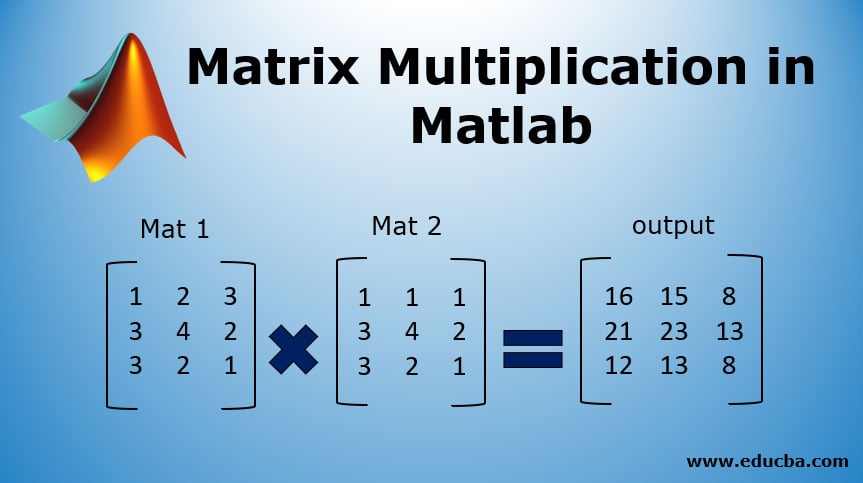
Matrix Multiplication In Matlab How To Perform Matrix Multiplication
The Singular Value Decomposition Guzinta Math

The Identity Matrix And Its Properties Mathbootcamps

The Identity Matrix And Its Properties Mathbootcamps
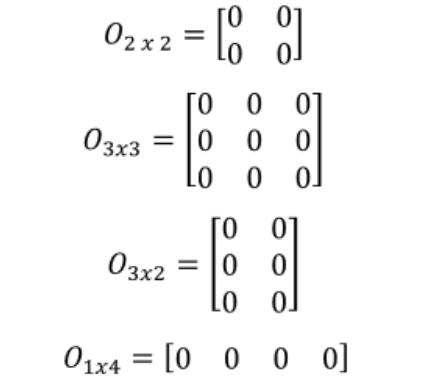
Definition Of A Zero Matrix Studypug
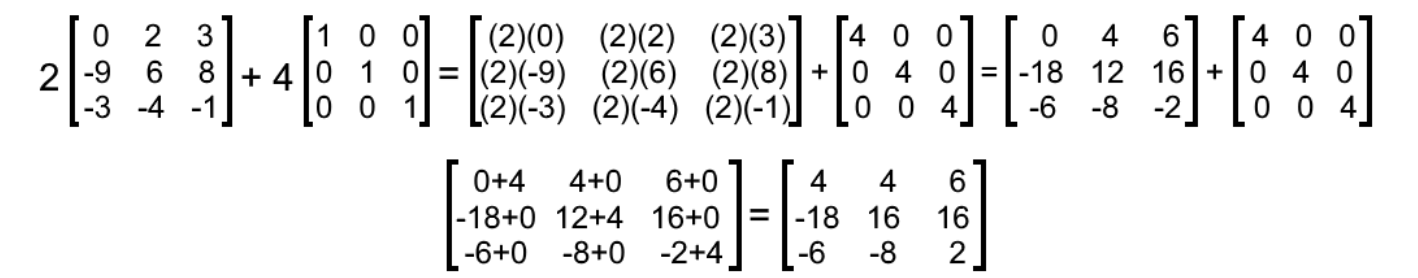
What Is An Identity Matrix Studypug
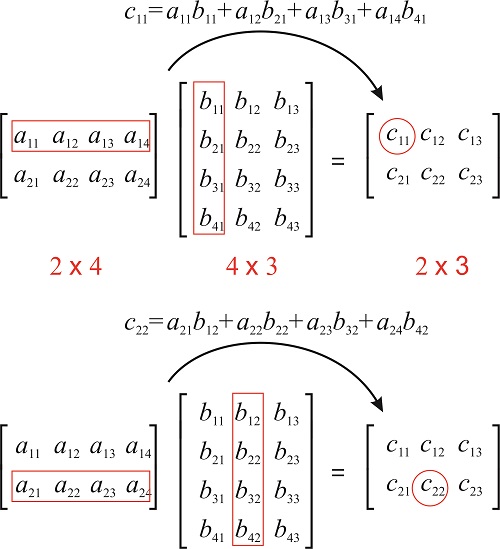
4 3 1 Matrices Chemistry Libretexts
Basic Linear Algebra For Deep Learning By Niklas Donges Towards Data Science

Solved When You Multiply A Matrix By The Identity Matrix Chegg Com
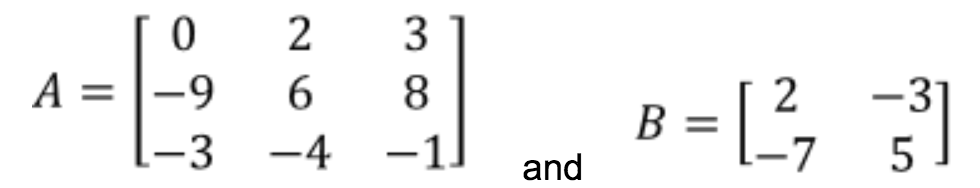
What Is An Identity Matrix Studypug

What Is An Identity Matrix Studypug
Multiplying Matrices Article Matrices Khan Academy

The Identity Matrix And Its Properties Mathbootcamps