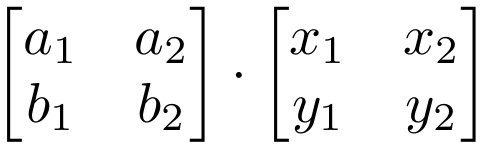Matrix Multiplication Using Outer Product
Denotes tensor product outer product Let e_t be the task indicator vector e_t00100T which is an one-hot encoded vector where only the t-th element is 1 and the rest elements are all zeros. Insteadof this one should think of matrix multiplication as returning a matrix that equals the sum of outerproducts of columnsofAand the correspondingrowsofB ie as the sum of rank-one matricesRecall that where eachAiBi2Rmp ABXAiBi.
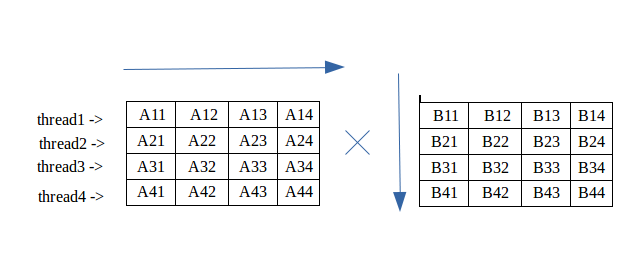
Multiplication Of Matrix Using Threads Geeksforgeeks
In the animation below in each time step we generate an outer product ie.
Matrix multiplication using outer product. The outer product usually refers to the tensor product of vectors. In addition to multiplying a matrix by a scalar we can multiply two matrices. If you want something like the outer product between a m n matrix A and a p q matrix B you can see the generalization of outer product which is the Kronecker product.
The algorithm involves Onm operations. A 1 n B a m 1 B. This involves multiplying the ith column of the first matrix Awith the ith row of the second matrix B for all i.
Where eachAiBj 2Ris a number computed as the inner product of two vectors inRn. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators. A m n B.
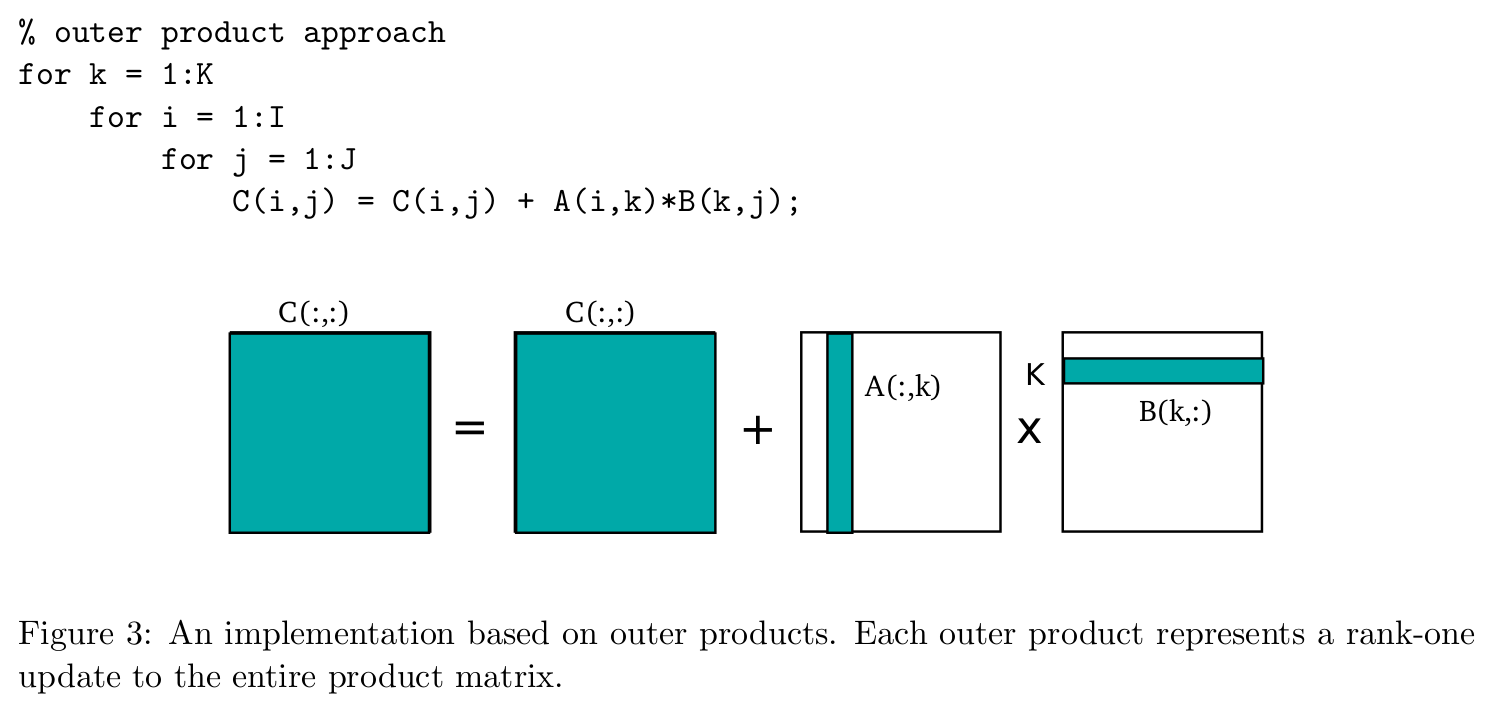
To my mind it is useful in several ways. If latexAlatex is an latextext mtext times text rtext latex matrix and latexBlatex is an latextext rtext times text ntext latex matrix then the product matrix. One way to design a matrix multiplication accelerator is to generate and accumulate partial sums in parallel.
More precisely we consider the C AB multiplication where all three matrices are square of dimensions NN. We generate M N partial sums in parallel. This entire MemFold composes the second stage of the outermost pipeline.
Finding the product of two matrices is only possible when the inner dimensions are the same meaning that the number of columns of the first matrix is equal to the number of rows of the second matrix. In matrix multiplication since each of the input matrices can be accessed in either a row-major order or column-major order there are four possible ways to perform matrix multiplication inner product row times column outer product column times row row-wise product row times row and column-. The outer product of two vectors xy which do not need to have the same dimension is often written x yT or with more details beginpmatrix x_1 x_2 vdots x_n endpmatrix cdot.
The outermost loop here is iterating across the inner matching dimensions of partial matrices. Generating partial sums is the same as computing an outer product of a column vector from A and a row vector from B. 2-D Data Distribution For this module we use a 2-D block data distribution.
Spectral decomposition which also leads you towards projectors as required for measurements. To work with the unconventional outer product-based matrix multiplication approach 1460. With decreasing matrix density the outer product al-gorithmmustovercometwooverheadswithincreasing matrixdimensionNthedecreasingnumberofuseful operations performed at each matrix datum and the increasing number of book-keeping operations due to thegrowingsizeofthedatastructureinFigure2.
I prove this identity. Update matrix A with multiplication of two vectors Algorithm for outer product update. To implement the outer product matrix multiplication algorithm in a distributed memory manner using message passing.
So to me the root cause is matrix multiplication which is computed using the inner product. It is noted A B and equals. Each multiplication generates a partial product matrix and all the generated matrices are then accumulated element-wise to form the final result.
A B a 11 B. Here we perform matrix multiply on the two tiles by using outer products. Definition of an inner and outer product of two column vectorsJoin me on Coursera.
Matrix Multiplication as the Sum of Outer Products The transpose of a matrix times itself is equal to the sum of outer products created by the rows of the matrix. So if we have a weight matrix W for all tasks and w_t is the weight vector for task t then w_tWe_t. In other words kk is.
Outer Product Update with Vector Mult. One particularly natural way for expressing the matrices as you say is using the outer product.

Dense Linear Algebra Our Pattern Language
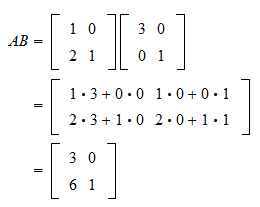
Matrix Multiplication And Linear Combinations

Illustration Of The General Algorithm For The Matrix Multiply Inner Download Scientific Diagram

Linear Algebra Matrix Multiplication Vs Dot Product Learnmath
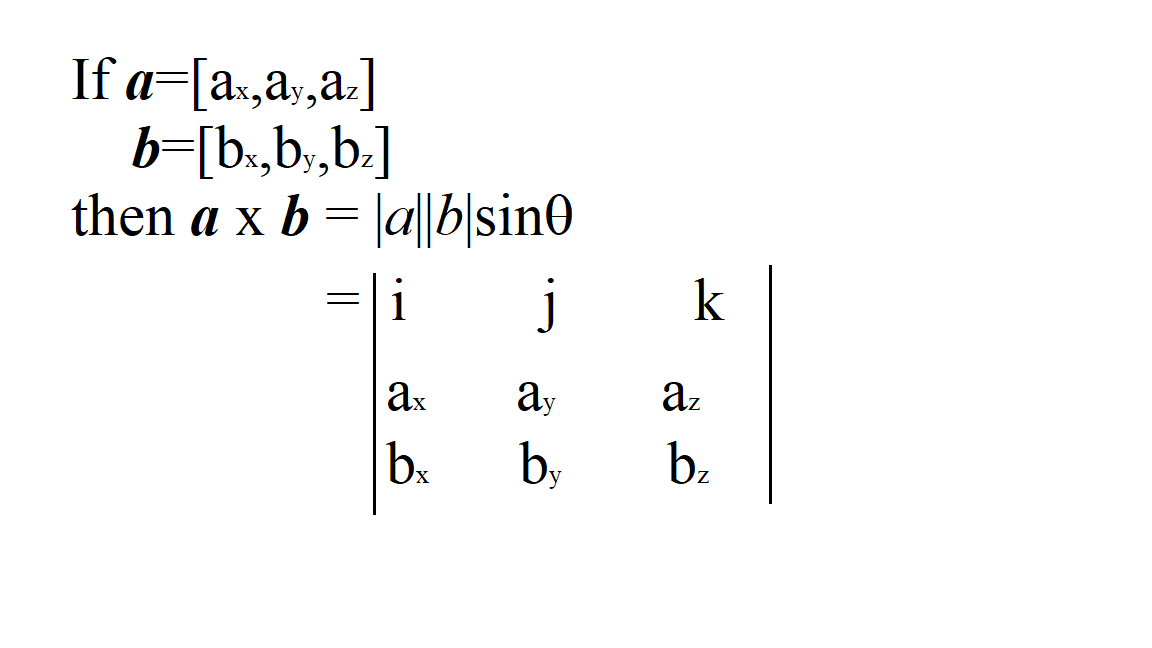
Numpy Vector Multiplication Geeksforgeeks

Vectorization In Python Geeksforgeeks
Matrix Matrix Multiplication Ml Wiki
Matrix Matrix Multiplication Ml Wiki
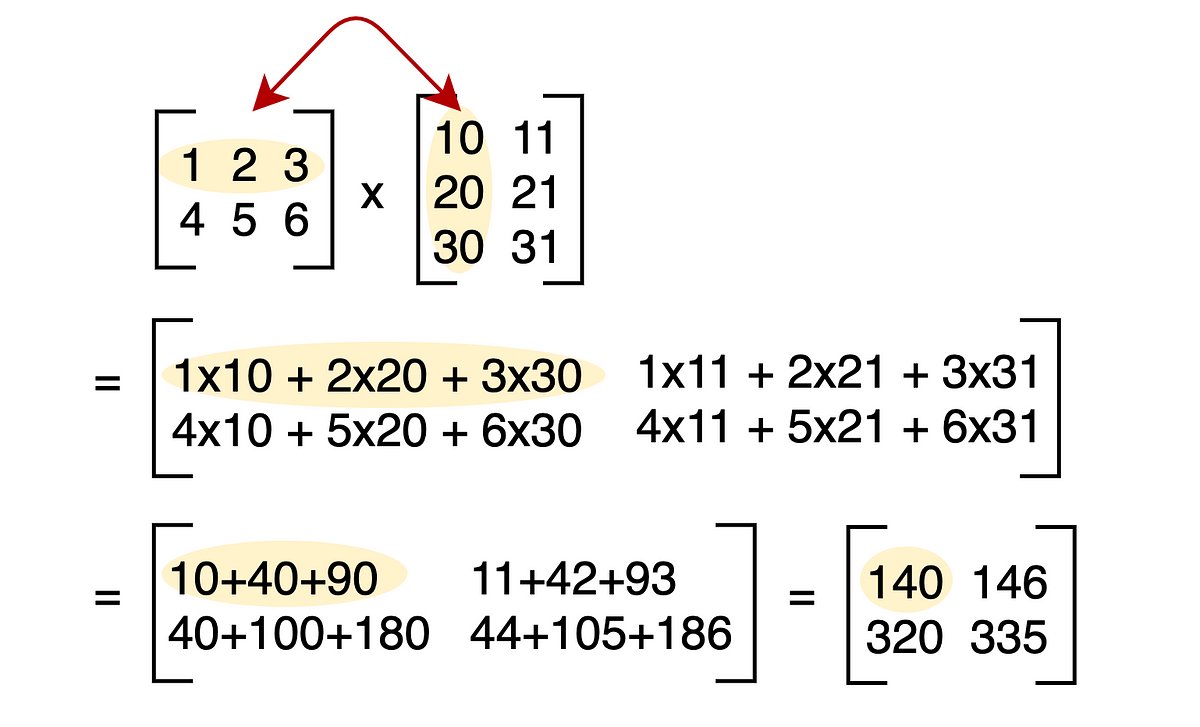
A Complete Beginners Guide To Matrix Multiplication For Data Science With Python Numpy By Chris The Data Guy Towards Data Science
Matrix Multiplication Calculator

Definition Of Outer Product Chegg Com
Http Blaauw Engin Umich Edu Wp Content Uploads Sites 342 2019 12 Outerspace An Outer Product Based Sparse Matrix Multiplication Accelerator Pdf

Definition Of Outer Product Chegg Com
Matrix Multiplication Identity Matrices More Transpositions
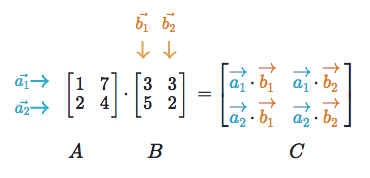
Linear Algebra Ml Glossary Documentation
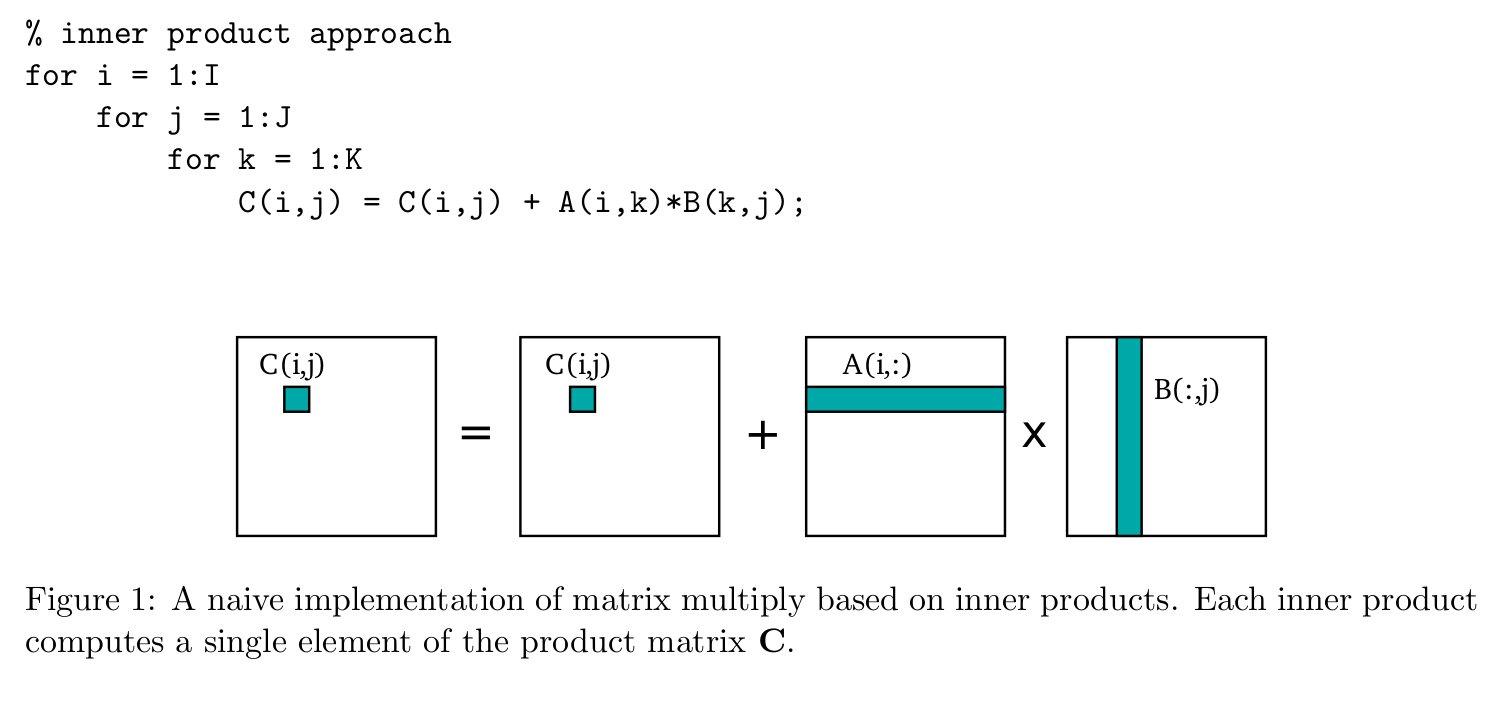
Dense Linear Algebra Our Pattern Language
Http Best Eng Buffalo Edu Research Lecture 20series 202013 Matrix 20multiplication Pdf
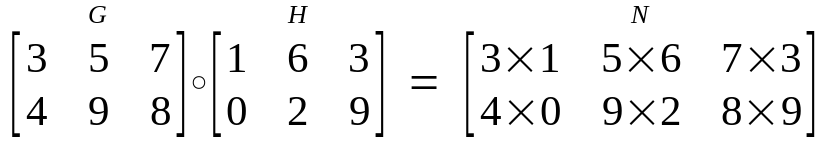
Part 14 Dot And Hadamard Product By Avnish Linear Algebra Medium
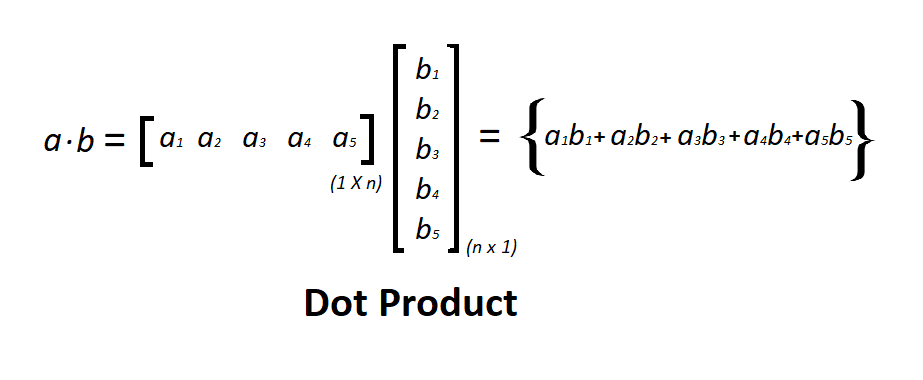
Vectorization In Python Geeksforgeeks