Matrix Multiply Loop Interchange

20 Sep, 2021

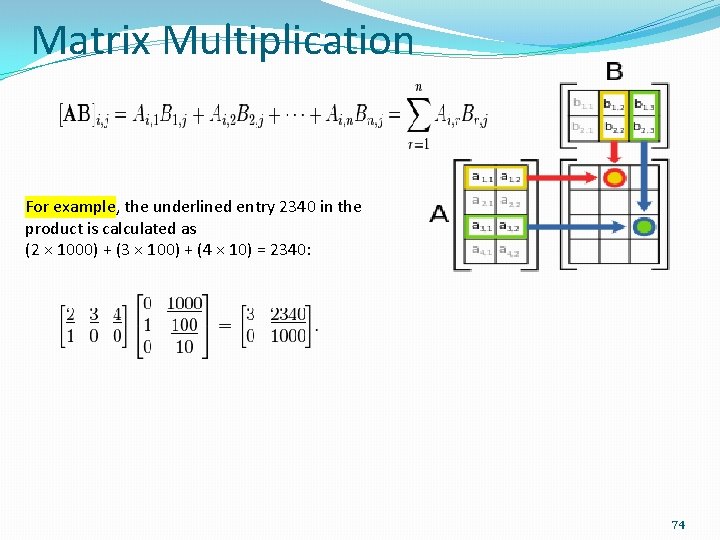
Next we show other variations of the matrix multiplication kernel that illustrate other RAJAkernel features. J cij cij aik bkj.

Mamas Computer Architecture Efficient Code Compiler Techniques And

Eration reordering checkers because it supports arbitrary loop tiling interchange etc and non-afﬁne transformations para-.

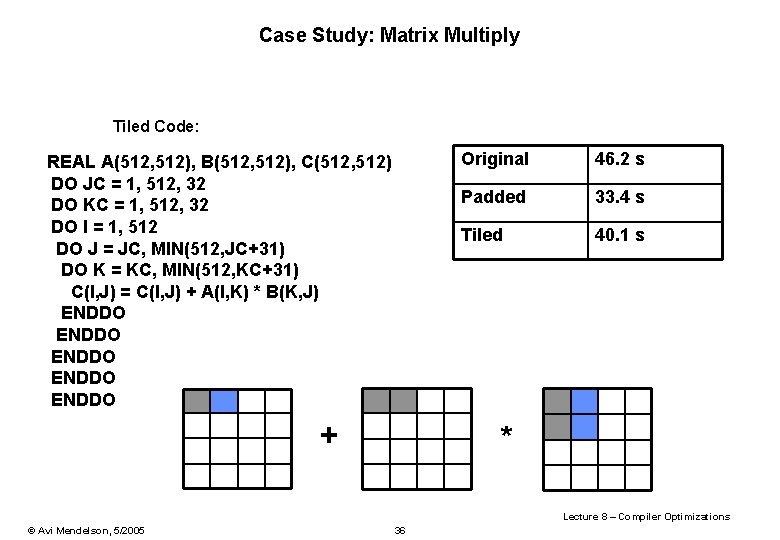
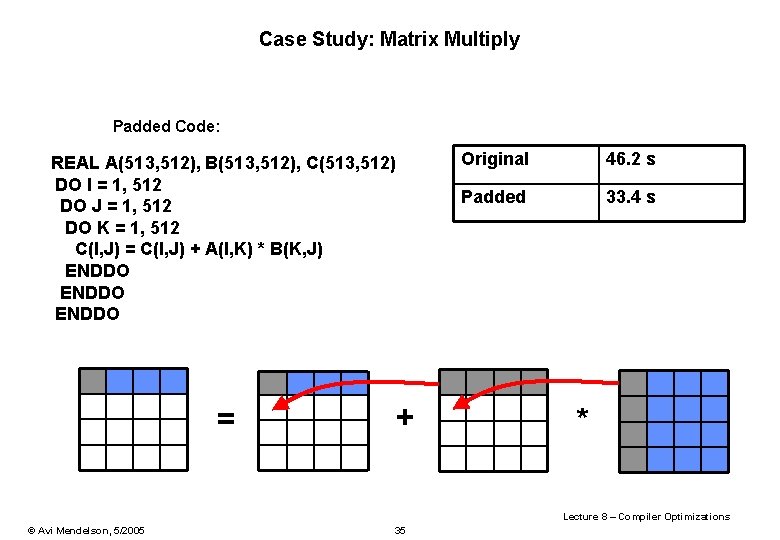
Matrix multiply loop interchange. The two inner loops read all p by n elements of B and access the same p elements in a row of A repeatedly and write one row of n elements of C. Often you find some mix of variables with unit and non-unit strides in which case interchanging the loops moves the damage around but doesnt make it go away. Experimental results on the Cray XD1 show that an FPGA-based matrix-multiplication design obtained us-ing the framework attains signiﬁcant speedup on the XD1s attached FPGA when compared to execution on the XD1 CPU.

Cray XMT Cray XMT-2 Matrix Multiply Dynamic Programming Multithreading Parallel. Consider matrix-matrix multiply when A is stored in column-major order ie each column is stored in contiguous memory for j 0. These improvements can be very signiﬁcant for production codes that run for extended periods of time.

They illustrate more complex policy examples and show additional RAJA kernel features. In this algorithm rather than streaming through all of the inputs you operate on a block at a time. Matrix multiplication with loop unrolling as well.

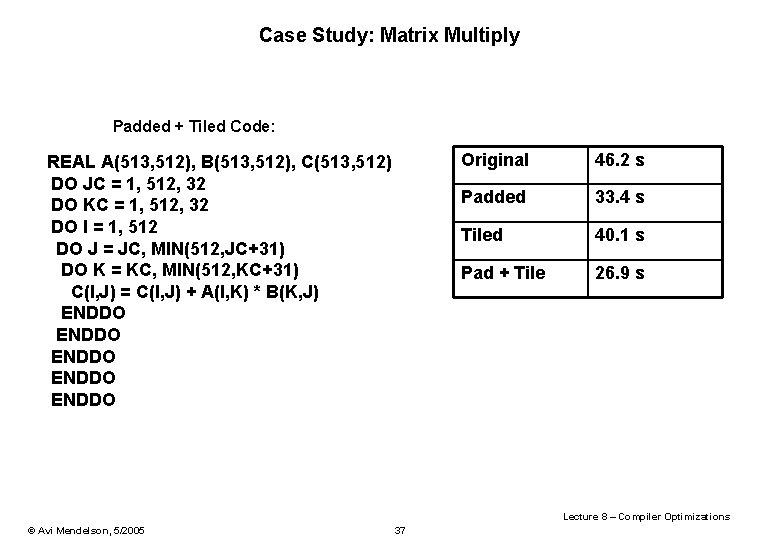
Similar to loop interchange there are multiple different ways you can choose to block the matrix multiplication algorithm. M n p and the size of the cache. However the irregular and matrix-dependent data access pattern of sparse matrix multiplication makes it challenging to use tiling to enhance data reuse.

Explicit blocking requires choosing a tile size based on these factors. The first example uses sequential execution for all loops. Clone via HTTPS Clone with Git or checkout with SVN using the repositorys web address.

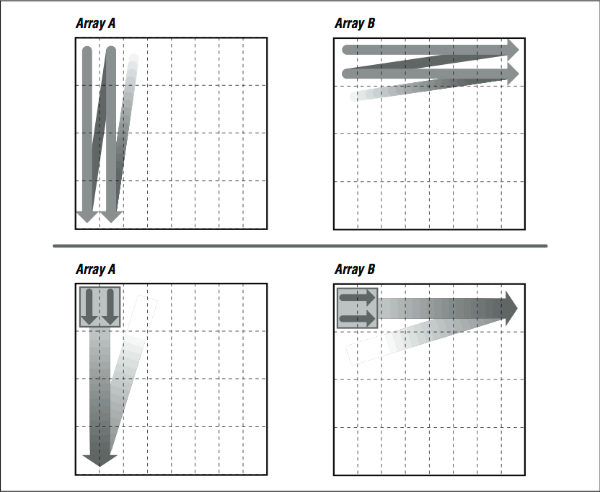
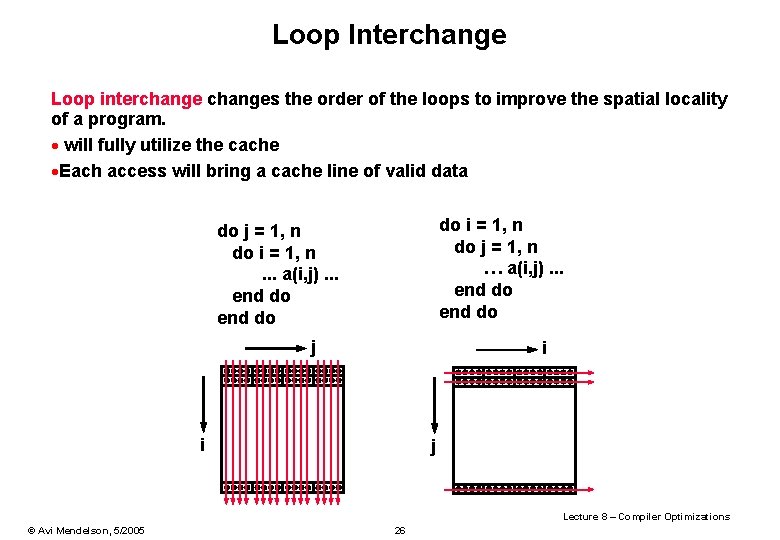
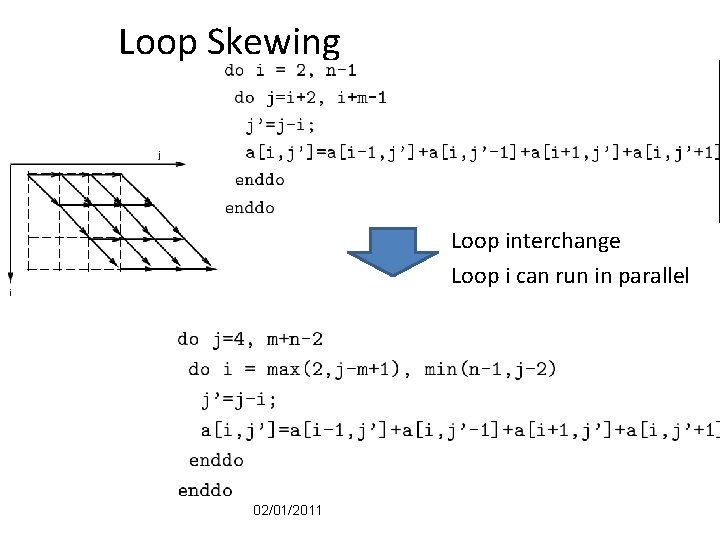
Space of problem sizes number of processors used and choices of loop parallelization can yield substantial improvements in performance. If the displacement loop is the outer one the 4 4 block of the actual image and a 12 4 region of the previous image must be kept in foreground if we work row-wise or column-wise to avoid duplicate transfers from background memory to the data-path. Loop interchange Change the order of a nested loop This is not always legal it changes the order that elements are accessed.

Matrix-matrix multiplication for multicoremanycore CPUs and GPUs. The best solution gives the tile sizes and tile-loop permutation to be used to generate. Edit the matrix multiply application by interchanging the two inner loops.

A Insert the elements at matrix1 using two for loops. Data reuse in tiled matrix multiplication off-the-shelf non-linear solver we use AMPL 9 with Ipopt 37 to produce optimal tile sizes and data movement costs here ranges over the levels of the memory hierarchy. The reason for this is that because the matrix is stored in row-major order each time you increment k youre skipping over an entire row of the matrix and jumping much further into memory possibly far.

Matrix Multiplication In Java Using For Loop 1 Condition for multiplication of two matrices is -1st matrix column number equal to 2nd matrix row number. If condition is true then. In ComputeV4 it is possible to interchange the loop which iterates over all possible displacements and the loop which scans over the 4 4 block itself.

Unfortunately life is rarely this simple. By contrast cache-oblivious algorithms are designed to make efficient use of cache without explicit blocking. C I J R.

In the matrix multiplication code we encountered a non-unit stride and were able to eliminate it with a quick interchange of the loops. Tion of parallel designs for some common nested loops are provided. This means that when running the innermost loop each iteration of the loop is likely to have a cache miss when loading the value of bkj.

R R A I K B K J. I yi Aij xj. Dynamic while the loop detector boundaries are fixed to facilitate comparison between the two data sources and aggregation of the transit data the plane of transit data is then discretized using the same cell boundaries from the loop detector matrix ie the.

In Nested Loop Interchange we provide a more detailed discussion of the mechanics of loop nest reordering. Tail testing a program multiplying two matrices where the input matrices are ﬁlled with zeros. The number of capacity misses clearly depends on the dimension parameters.

Why is this useful. You can improve the cache behavior of matrix multiplication by using a blocked algorithm. For example a buggy-transformed.

The order of loop nests loop interchange also plays an important role in achieving better cache performance. EQ 34 0 0 N i 0 1 1 0 0 0 i N. 2 Read rowcolumn numbers of matrix1 matrix2 and check column number of matrix1 row number of matrix2.

J for i 0. In this paper we devise an adaptive tiling strategy and apply it to enhance the performance of two primitives. The matrix multiplication kernel variations described in this section use execution policies to express the outer row and col loops as well as the inner dot product loop using the RAJA kernel interface.

Categories and Subject Descriptors C13 Processor Ar-. For example if we want to interchange the loops putting j in the outer loop and i in the inner loop we can multiply the loop nest matrix by an interchange matrix as follows.

Https Passlab Github Io Csce513 Notes Lecture10 Localitymm Pdf