Symmetric Matrix Lu Decomposition
I A2R n is called symmetric positive de nite if A AT and vT Av0 for all v2Rn v6 0. The Band LU Decomposition The BandLUDecomposition class represents the LU decomposition of a band matrix.
Https Webpages Uncc Edu Krs Courses 4133 5133 Lectures Lu2 Pdf
It hinges on the observation that a tridiagonal matrix is up to a rank 1 perturbation a block diagonal matrix.

Symmetric matrix lu decomposition. The equation L1U1 L2U2 can be written in the form L 1 2 L1 U2U 1 1 where by lemmas 12-14L1 2 L1 is unit lower triangular and U. A necessary and sufficient condition for a symmetric matrix to be positive definite is given later in this section. I If A2R n is symmetric positive de nite then the LU decomposition can be computed in a stable way without permutation ie A LU I Can we use the structure of A ie.
One can then find the eigendecomposition of the sub-blocks in parallel and glue them back together using a. I A2R n is called m- banded if a ij 0 for ji jjm. Grinfelds Tensor Calculus textbookhttpslemmaprep - C.
If bne r cne s you indeed get the LU decomposition ALUbeginbmatrix 1 0 0 0 -a 1 0 0 -a 0 1 0 -a 0 0 1 endbmatrix beginbmatrix arrr 0b-rs-rs-r 00c-sb-s 000d-b endbmatrix The conditions ane0 and dne b are irrelevant. And j 1 ITCS 41335133. Every symmetric positive definite matrix A can be decomposed into a product of a unique lower triangular matrix L and its transpose.
To Numerical Methods 17 LUQR Factorization. X Suppose A L1U1 L2U2 are two LU-factorizations of the nonsingular matrix A. The matrix L Ln1 L1 1 is exactly what one would compute in an LU de-composition of an arbitrary matrix.
And it requires less storage space than the general decomposition. Let A be symmetric and A LDU be a LU-decomposition of A where D is a diagonal matrix and u_ii 1. Matrix decomposition is a fundamen-.
The LU-factorization of a nonsingular matrix is unique whenever it exists. To take advantage of the special structure of band matrices two special classes are defined that represent the LU decomposition of a general band matrix and the Cholesky decomposition of a symmetric band matrix. It is applicable to symmetric tridiagonal matrices but any matrix can be reduced to such a form via the Lanczos method.
Symmetric Positive De nite Matrices I A2R n is called symmetric if A AT. A LDU LDUT UTDLT. Matrix decomposition refers to the transformation of a given matrix into a given canonical form 1 when the given matrix is transformed to a right-hand-side product of canonical matrices the process of producing this decomposition is also called matrix factorization.
Hermitian positive-definite matrix and thus also every real-valued symmetric positive-definite matrix has a unique Cholesky decomposition2 If the matrix A is Hermitian and positive semi-definite then it still has a decomposition of the form A LL if the diagonal entries of L are allowed to be zero3. HttpsbitlyPavelPatreonhttpslemmaLA - Linear Algebra on LemmahttpbitlyITCYTNew - Dr. This means LDUT is another LU-decomposition of A.
To see this we use elementary matrices. Every Hermitian positive-definite matrix and thus also every real-valued symmetric positive-definite matrix has a unique Cholesky decomposition. A L LT.
For j 23i 1. In an ordinary LU decomposition when clearing the first column each row replace-ment involves n 1 multiplications scale the first row and n 1 additions add to the. The associated solution method is known as Choleskys method.
UT is a lower left triangular matrix and LT is a upper right triangular matrix. 72 LU Decomposition of Symmetric Matrices Given the symmetric structure of the LDU factors of a symmetric matrix see Section 71 and the common use of LU factorization in the analysis of linear systems it is constructive to develop expressions that relate an explicit LU decomposition to an implicit LDU factorization. This means the decomposition is unique.
Let A be a symmetric positive-definite matrix. For i 23n l ij a ij P j 1 k1 l ikl jk l jj. However one can save compute cycles by taking advantage of the symmetry of S.
There is a unique decomposition such that A L L T where L is lower-triangular with positive diagonal elements and L T is its transpose. To find and in an decomposition of we can try to use row reduction. LU Decomposition We can use Cholesky Decomposition to compute the LU decompo-sition of A l 11 p a 11 l ii v u u ta ii Xi 1 k1 l2 ik.

Chapter 2 Matrices 2 1 Operations With Matrices
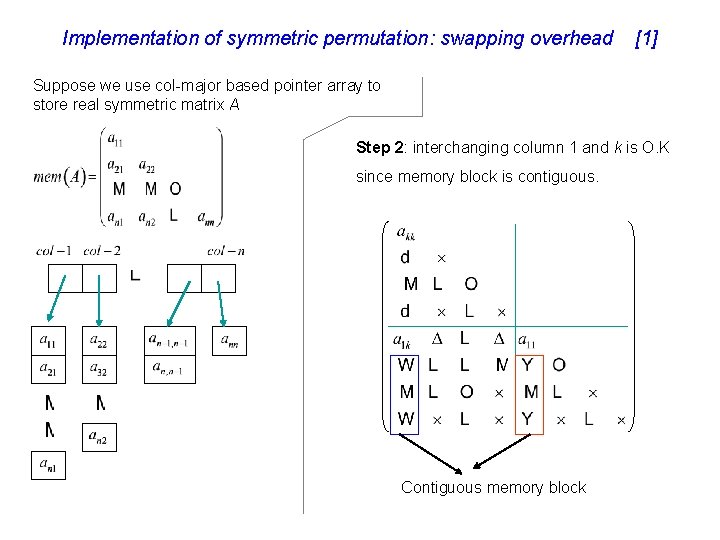
Chapter 13 Gaussian Elimination Iii Bunchparlett Diagonal Pivoting
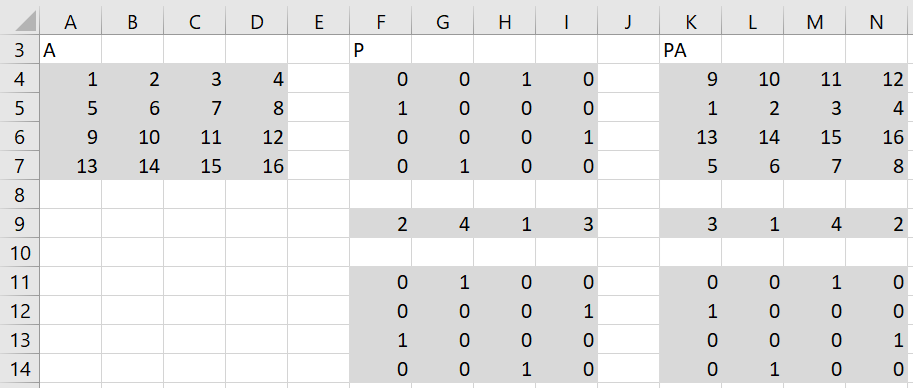
Lu Factorization Real Statistics Using Excel

Similar Diagonalization Of Real Symmetric Matrix Ppt Video Online Download

Chapter 13 Gaussian Elimination Iii Bunchparlett Diagonal Pivoting

Chapter 13 Gaussian Elimination Iii Bunchparlett Diagonal Pivoting

Symmetric Matrices And Quadratic Forms Ppt Download
Https Webpages Uncc Edu Krs Courses 4133 5133 Lectures Lu2 Pdf

Chapter 10 Lu Decomposition Ppt Video Online Download

Symmetric Matrices And Quadratic Forms Ppt Download

Similar Diagonalization Of Real Symmetric Matrix Ppt Video Online Download

Symmetric Matrices And Quadratic Forms Ppt Download

Chapter 13 Gaussian Elimination Iii Bunchparlett Diagonal Pivoting

Symmetric Matrices And Quadratic Forms Ppt Download

Symmetric Matrix Decomposition For A Ldu Ldl With Elementary Matrices Youtube
Https Webpages Uncc Edu Krs Courses 4133 5133 Lectures Lu2 Pdf

Linear Algebra Matrix Eigenvalue Problems Part 2 Ppt Download

Chapter 13 Gaussian Elimination Iii Bunchparlett Diagonal Pivoting

Lu Decomposition Algorithm Is Presented In A The Resulting Matrices Download Scientific Diagram