Three Matrix Multiplication Complexity
Matrix Multiplication Vectorized implementation. Begingroup It is obvious that the proposed divide and conquer approach has worst-case complexity Olg n only when the matrix order is O1 since in this case the corresponding recurrence equation is Tn Tn2 O1 as an example for a 3 x 3 matrix a matrix multiplication can be done using a constant number of scalar multiplications and additions.
The best known algorithm has complexity approximately O n23728639.
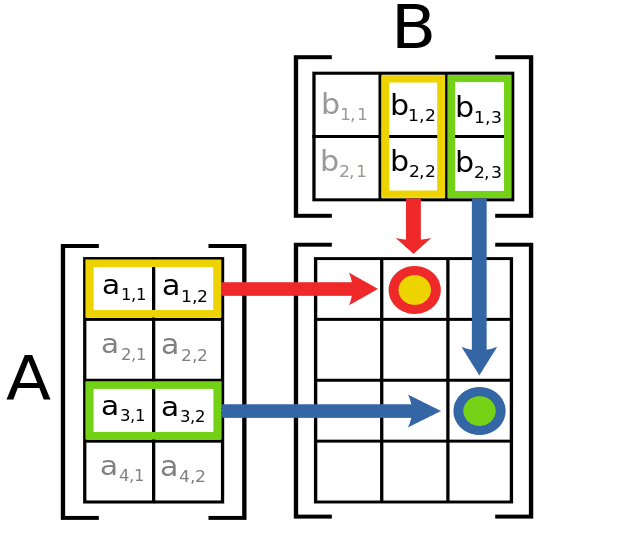
Three matrix multiplication complexity. AxB Matriks Diketahui Matriks A Beginpmatrix 2 1 1 3 4 3endp Gauthmath - Online calculator to perform matrix operations on one or two matrices including addition subtraction multiplication and taking the power determinant inverse or transpose of a matrix. For the multiplication of two matrix one can use the classical methods such as strassen algorithm to reduce the time complexity. In particular we obtain the improved lower bound of 19 for the bilinear complexity of.
A nparray 123 456 B nparray 123 456 print Matrix A isnA print Matrix A isnB C npmultiply AB print Matrix multiplication of matrix A and B isnC The element-wise matrix multiplication of the given arrays is calculated in the following ways. On top of that the R matrix will first have to be copied into interleaved complex format imaginary part 0 before the complex matrix multiply routines can be called. The main condition of matrix multiplication is that the number of columns of the 1st matrix must equal to the number of rows of the 2nd one.
As a result of multiplication you will get a new matrix that has the same quantity of rows as the 1st one has and the same quantity of columns as the 2nd one. However it is unknown what the underlying complexity actually is. Sum_k1N x_kitimes SX_kj.
This would yield a complexity of ODNDN as user7530 explained. In matrix multiplication there are 3 for loop we are using since execution of each for loop requires time complexity On. So for three loops it becomes On3.
In this program we have to use nested for loops to iterate through each row and each column. We also use these results to construct a new algorithm which shows that omega 2495548. While this video is m.
We use zip in Python. For example if you multiply a matrix of n x k by k x m size youll get a new one of n x m dimension. Here we assume that integer operations take O1 time.
These videos are for the data structures and object oriented programming in C class CSCI 104 I am teaching at USC during Fall 2020. For example one can precompute the matrix SX_kj whose values will be reused for the matrix-vector multiplications in the rest of the product. Here I just wonder if there is any efficent algorithm aiming at the multiplication of three matrix.
Up to 10 cash back In 1976 Laderman proposed a noncommutative algorithm to calculate the multiplication of two 3times 3 matrices and it requires 23 multiplications 7 which improves the previous attempts by Gastinel 8 25 multiplications and Hopcroft and Musinski 9 24 multiplications. So you get that additional burden twice in fact but this may be somewhat offset by the speed of doing a lot of 0 multiplies. Namely For D ABC Or specially D OTBO where T represents for transposition.
There are three for loops in this algorithm and one is. We prove a lower bound of 2 mn 2 n m 2 for the bilinear complexity of the multiplication of n m -matrices with m n -matrices using the substitution method m n 3. Matrix-Multiplication X Y Z for i 1 to p do for j 1 to r do Zij 0 for k 1 to q do Zij Zij Xik Ykj Complexity.
Please try your approach on IDE first before moving on to the solution. With the formula above the answer to your last question is straightforward. A consequence of these results is that omega the exponent for matrix multiplication is a limit point that is it cannot be realized by any single algorithm.
Matrix Multiplication Using Nested List. The naive algorithm has complexity O mjn for multiplying an m x j matrix by a j x n matrix or O n3 for square n x n matrices. There are three generic matrix multiplies involved.

Decision Making Algorithms Google Search

A Matrix Of Feedback For Learning A Brief Summary Feedback Learning Pd Resources
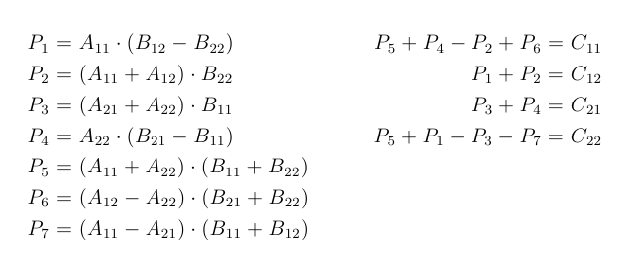
Strassen Matrix Multiplication C The Startup

Time Complexity Of Some Matrix Multiplication Mathematics Stack Exchange
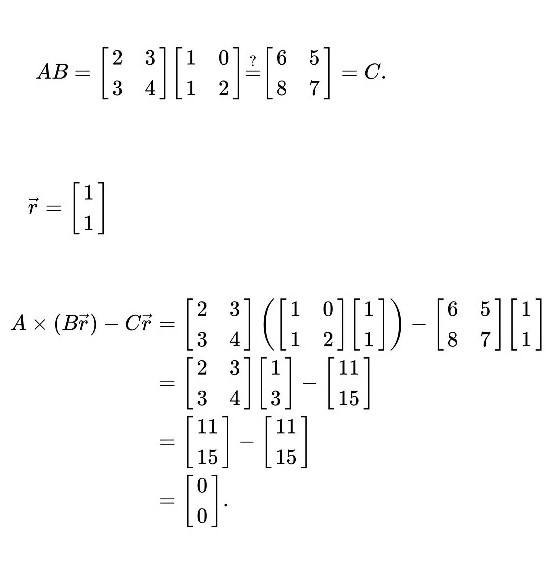
Freivalds Algorithm For Verifying Matrix Multiplication

Tool To Distinguish Between Depth Of Knowledge Levels Robert Kaplinsky Glenrock Consulting Llc Depth Of Knowledge Secondary Math Knowledge

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

The Fourier Transform Can Be Computed As A Matrix Multiplication Physics And Mathematics Cool Math Tricks Math Tricks

Computing Flops For Matrix Multiplication Mathematics Stack Exchange

Introduction To Matrices And Matrix Arithmetic For Machine Learning

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Pre Defined Sparsity For Reducing Complexity In Neural Networks Networking Deep Learning Smart System

Matrix Multiplication Example 3 3x3 By 3x1 Youtube

Numpy 3d Matrix Multiplication Geeksforgeeks





