Why Does Matrix Multiplication Work The Way It Does
For matrix multiplication to work the columns of the second matrix have to have the same number of entries as do the rows of the first matrix. So if you did matrix 1 times matrix 2 then b must equal c in dimensions.
A Complete Beginners Guide To Matrix Multiplication For Data Science With Python Numpy By Chris The Data Guy Towards Data Science
BA is the their reverse composition.
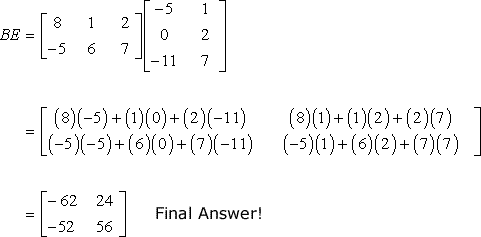
Why does matrix multiplication work the way it does. Matrix multiplication is equivalent to composition of linear transformations between finite dimensional vector spaces. This is what motivates matrix multiplication and why it works the way it does. At its most fundamental level a matrix transforms a vector by scaling it in some fashion.
Lets give an example of a simple linear transformation. Then write down their matrix representations in some basis and multiply those matrices. I think the dot product is a distraction here a convenient way to express the result rather than some intrinsic property.
Suppose my linear transformation is. The main reason why matrix multiplication is defined in a somewhat tricky way is to make matrices represent linear transformations in a natural way. View the full-size image 14.
In your case inner dimensions do not match. Matrix multiplication is not universally commutative for nonscalar inputs. Write down your two favorite linear transformations and compose them.
Imagine as a coordinate in 2D space as usual. It explains why matrix multiplication is the way it is instead of piecewise multiplication. The MMULT function appears in certain more advanced formulas that need to process multiple rows or columns.
If you had matrix 1 with dimensions axb and matrix 2 with cxd then it depends on what order you multiply them. Kind of like subtraction where 2-3 -1 but 3-21 it changes the answer. Matrix multiplication is NOT commutative.
There is a special case involving Simultaneous Diagonalization and when both matrices are diagonal but that is beyond this. Multiplying matrices is meant to represent composing the linear functions that those matrices represent. Why does the second matrix have to be oriented completely different from the first matrix to make the multiplication happen.
The composition of two linear functions is a linear function. If at least one input is scalar then AB is equivalent to AB and is commutative. Rows come first so first matrix provides row numbers.
Heres a matrix that multiples the x y and z components of a vector by different scale factors. Multiplying two matrices represents applying one transformation after anotherHelp fund future projects. Because matrix multiplication is such a central operation in many numerical algorithms much work has been invested in making matrix multiplication algorithms efficient.
The problem with having both matrices oriented the same way is that then we would have no system for determining which cell in the result matrix we should store the result of performing the dot product of two vectors. If a linear function is represented by A and another by B then AB is their composition. The reason why tfmatmul does not work the way you expected is written in the documentation.
In your case you have a matrix y and a tensor x rank 3 2. This are just simple rules to help you remember how to do the calculations. The only sure examples I can think of where it is commutative is multiplying by the identity matrix in which case BI IB B or by the zero matrix that is 0B B0 0.
So if A represents the linear function f x and B represents the linear function g x AB is mean to represent the linear function f g x. The MMULT function returns the matrix product of two arrays sometimes called the dot product. Just as with adding matrices the sizes of the matrices matter when we are multiplying.
The result from MMULT is an array that contains the same number of rows as array1 and the same number of columns as array2. To multiply matrices they need to be in a certain order. C mtimes AB is an alternative way to execute AB but is rarely used.
That is AB is typically not equal to BA. Thats one way of thinking of it. From a modern perspective matrix multiplication is defined the way it is in order to correspond to composition of linear transformations but historically the concept of linear substitutions came first.
The inputs must be matrices or tensors of rank 2 representing batches of matrices with matching inner dimensions possibly after transposition.
Scalar Multiplication In R Stack Overflow
Sparse Matrix Multiplication Description By Glyn Liu Medium
Matrix Multiplication Chilimath
Why Does Matrix Multiplication Work The Way It Does By Erik Engheim Medium
Multiplying Matrices By Scalars Article Khan Academy
Matrix Multiplication In C Applying Transformations To Images
Why Does Matrix Multiplication Work The Way It Does By Erik Engheim Medium
How To Multiply Two Matrices Together Studypug
Matrix Multiplication Free Math Help
Why Does Matrix Multiplication Work The Way It Does By Erik Engheim Medium
Intro To Matrix Multiplication Video Khan Academy
Why Does Matrix Multiplication Work The Way It Does By Erik Engheim Medium
Why Does Matrix Multiplication Work The Way It Does By Erik Engheim Medium
Breakthrough Faster Matrix Multiply
Multiplying Matrices Article Matrices Khan Academy
How To Multiply Matrices Quick Easy Youtube
How To Multiply Matrices A 3x3 Matrix By A 3x3 Matrix Youtube
