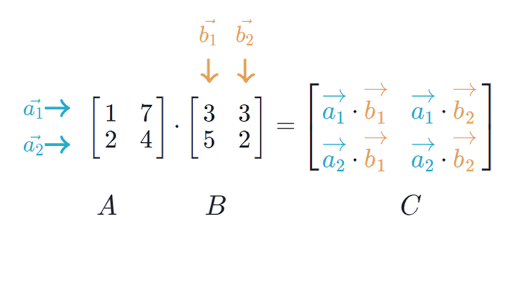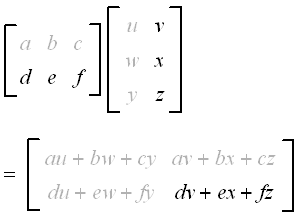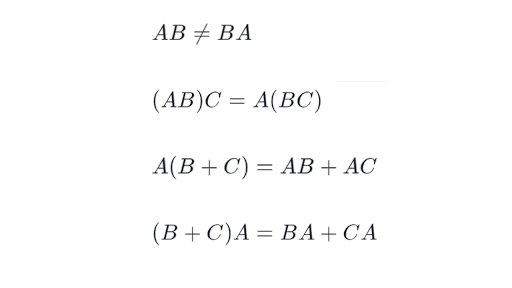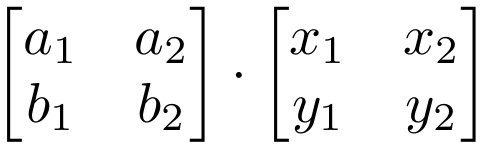Matrix Multiplication Right To Left
If you multiply from the left eg. XA x you need to swap the second and third row.
Multiplying Matrices Article Matrices Khan Academy
With no parentheses the order of operations is left to right so AB is calculated first which forms a 500-by-500 matrix.
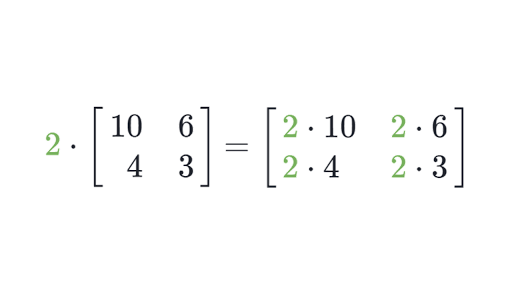
Matrix multiplication right to left. A matrix with 2 columns can be multiplied by any matrix with 2 rows. 2 x 3 times 3 x 3. It depends if you transform your points by multiplying the matrix from the left or from the right.
Matrix E right number of rows 3. Since this is the case then it is okay to multiply them together. As expected this is upper triangular and in fact the same as the U matrix returned by the Julia lu function above.
This allows matrices to represent linear transformations more intuitively. 12 April 1 Introduction In this assignment you will write code to multiply two square n n matrices of single precision floating point numbers and then optimize the code to exploit a memory cache. A b a T b displaystyle left mathbf a cdot mathbf b rightmathbf a operatorname T mathbf b which is written as ai bi in Einstein summation convention.
If you multiply from the right eg. Due to the matrix multiplication rules not all matrices can be multiplied. The dot product of two column vectors a and b can be computed as the single entry of the matrix product.
Representing the columns of X by colorful boxes will help visualize this. Smathtt Rcdot mathbf xmathtt Rscdot mathbf x. Matrix multiplication is defined so that it works right to left just like function composition.
Matrix Multiplication and Cache Friendly Code COMP 273 Winter 2021 Assignment 4 Prof. Transformations and matrix multiplication. Now these are the steps.
Sticking the white box with a in it to a vector just means. F x g y f f 1 x g f 1 y. What is obtained on the right is the inverse of the original matrix.
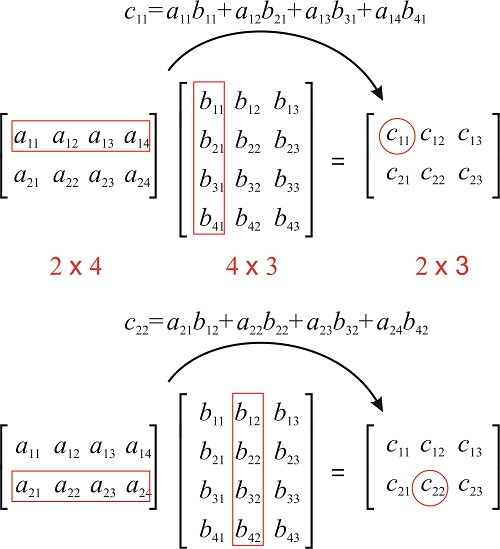
If you instead specify A BC then BC is multiplied first producing a 2-by-2 matrix. 24 March Due date. E E to have a product the number of columns of left matrix B must equal the number of rows of right matrix E.
If any one of these is changed such as rotating axes instead of vectors a passive transformation then the inverse of the example matrix should be used which coincides with its transpose. An easy way to determine this is to write out each matrixs rows x columns and if the numbers on the inside are the same they can be multiplied. F n F m L A x A x for any x F n which is a left-multiplication transformation defined using a matrix A.
Because matrix multiplication is generallynot commutative E. Use elementary row operations so that the identity appears on the left. It is E 2E 1A not E 1E 2A.
Place them side by side. Multiplication of two matrices is defined if and only if the number of columns of the left matrix is the same as the number of rows of the right matrix. The examples in this article apply to active rotations of vectors counterclockwise in a right-handed coordinate system y counterclockwise from x by pre-multiplication R on the left.
Compositions of linear transformations 1. Multiply this vector by the scalar a. This matrix is then multiplied with C to arrive at the 500-by-2 result.
Its also why we conventionally represent vectors as column matrices. Matrix up here but what is this equal to this this right here by definition this is the matrix a times the matrix B right the definition of matrix products is you take the first matrix and multiply times the column vectors of the second Matrix and by the. Since I havent decided which are the two bases to be used to represent those x F n L x F m how to even compute the multiplication A x.
Two matrices can only be multiplied if the number of columns of the matrix on the left is the same as the number of rows of the matrix on the right. Matrix B left number of columns 3. Write the original matrix augmented with the identity matrix on the right.
But its confusing that a left-multiplication transformation is defined using a matrix and need the idea of matrix multiplication. E 2zE 1 E A U Notice that we multiplied A by the elimination matrices from right to left in the order of the steps. Lets begin by looking at the right-multiplication of matrix X by a column vector.
Use matrix multiplication to show that AA1 I A A 1 I and A1A I A 1 A I. Mathtt T cdot left beginarrayc mathbf x 1endarray right left beginarrayc smathtt Rcdot mathbf x mathbf t 1endarray right Note that rotation and scaling commutes. These matrices may be multiplied by each other to create a 2 x 3 matrix.
Ax x where A is a matrix and x the transformed point you just need to swap the second and third column. If A is an m -by- n matrix and B is an n -by- p matrix then their matrix product AB is the m -by- p matrix whose entries are given by dot product of the corresponding row of A and the. The result is another column vector - a linear combination of X s columns with a b c as the coefficients.
In 24E2E1AU Out24true Thus we have arrived at the formula.
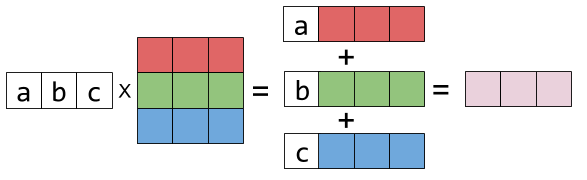
Visualizing Matrix Multiplication As A Linear Combination Dzone Big Data

A Complete Beginners Guide To Matrix Multiplication For Data Science With Python Numpy By Chris The Data Guy Towards Data Science
15 3 Matrix Multiplication Chemistry Libretexts

Multiplying Matrices Video Khan Academy

Codebox Create Image Filters With Matrix Multiplication Make
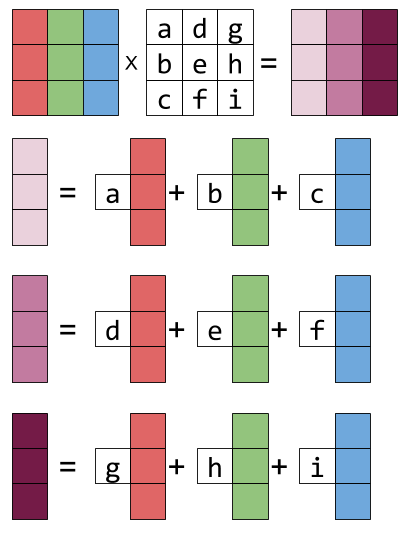
Visualizing Matrix Multiplication As A Linear Combination Dzone Big Data
Properties Of Matrix Multiplication Article Khan Academy
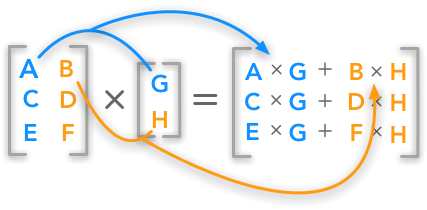
Introduction To Matrices And Vectors Multiplication Using Python Numpy
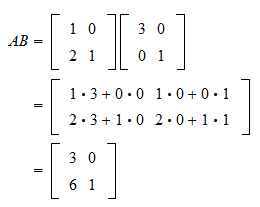
Matrix Multiplication And Linear Combinations
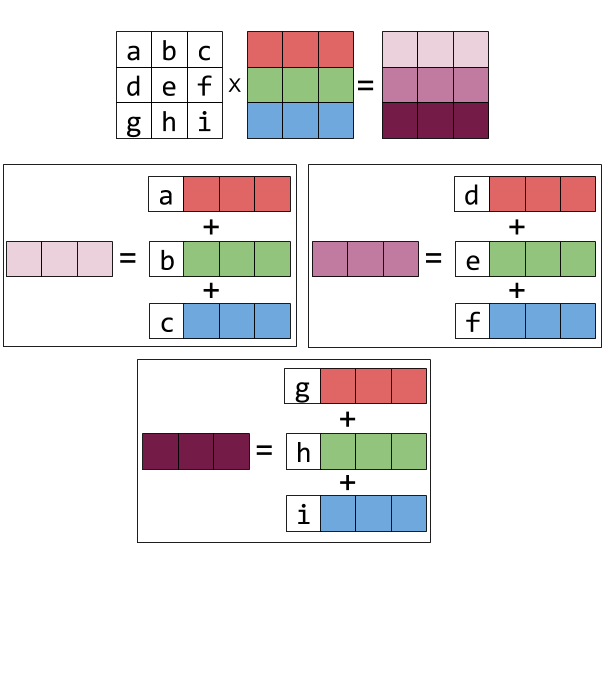
Visualizing Matrix Multiplication As A Linear Combination Dzone Big Data
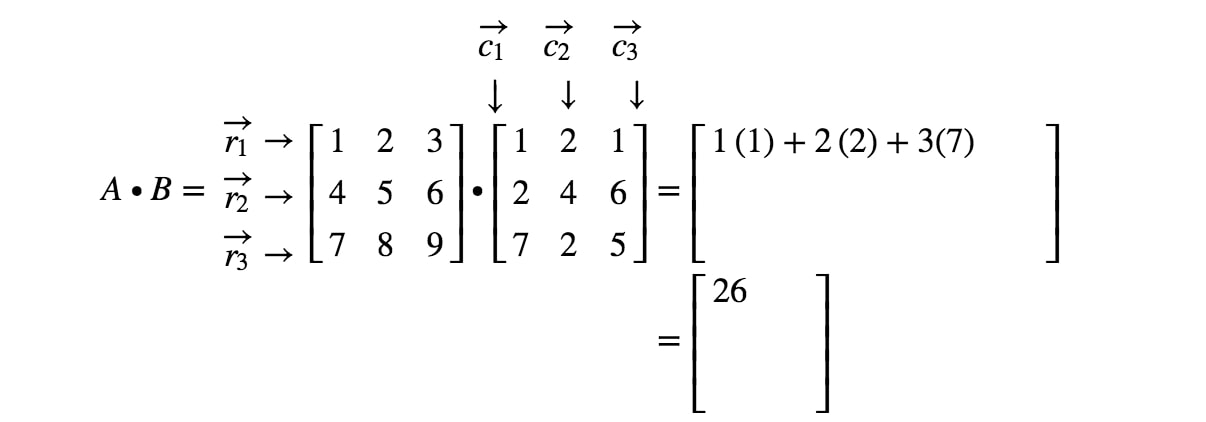
How To Multiply Two Matrices Together Studypug
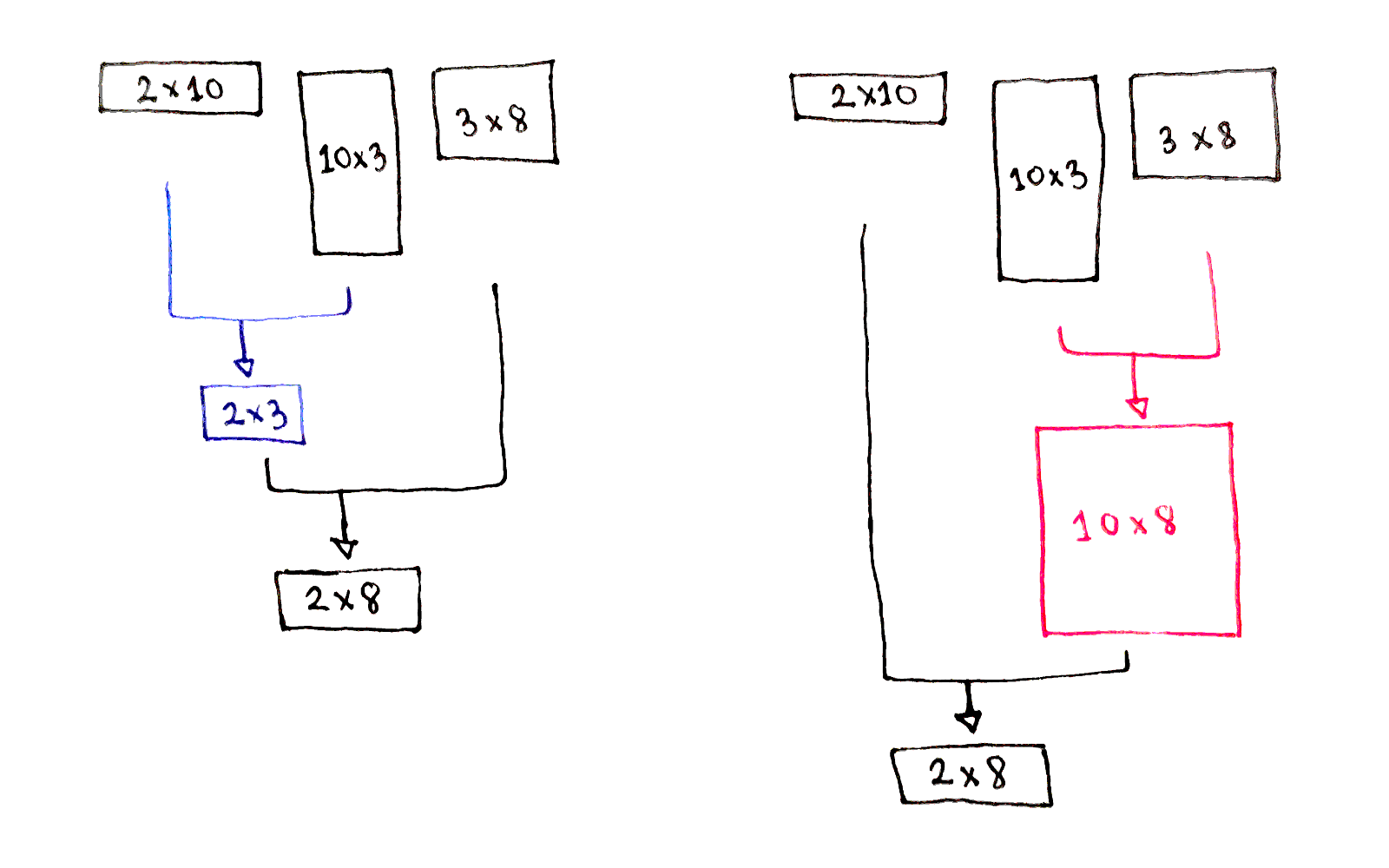
Dynamic Programming Deep Dive Chain Matrix Multiplication
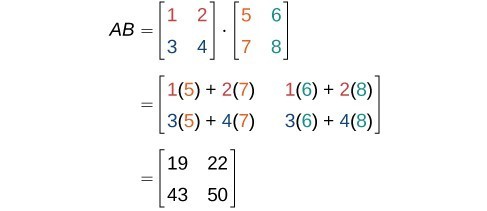
Finding The Product Of Two Matrices College Algebra
Matrix Multiplication Calculator
Multiplying Matrices By Scalars Article Khan Academy
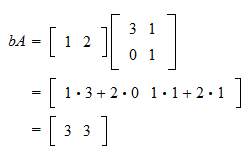
Matrix Multiplication And Linear Combinations
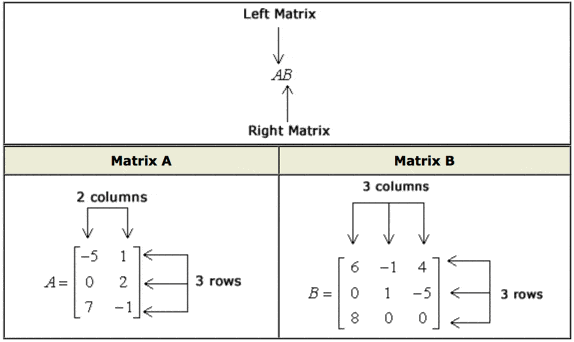
Matrix Multiplication Chilimath