What Does It Mean When A Matrix Does Not Have An Inverse
Singular matrices are matrix which has determinant zero and does not have inverse. You can verify that this matrix not.
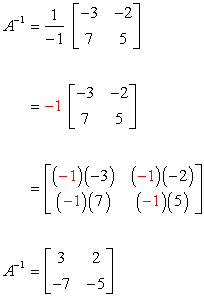
Inverse Of A 2x2 Matrix Chilimath
And the determinant lets us know this fact.
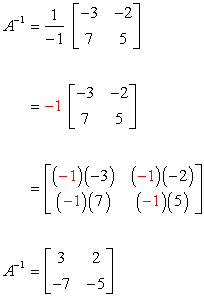
What does it mean when a matrix does not have an inverse. Whatever A does A 1 undoes. No if the coefficient matrix is not invertible the system could be inconsistent and have no solution or be dependent and have infinitely many solutions. A square matrix A has either no inverse or a unique inverse A-1.
If A is an nxn matrix and there exists some matrix B such that AB BA I where I is the identity. A matrix that does not have an inverse is called singular. The reason behind this is that let a non invertible matrix be reduced to the identity matrix by a series of row operation.
In this question we have to fill in the blank. Homework Statement Show that a matrix with a row of zeros cannot have an inverse. When a matrix doesnt have an inverse it means just that.
Such a matrix is called a singular matrix. The second row is just double the first row and does not add any new information. This Matrix has no Inverse.
Finding the Inverse the Hard Way. Not every matrix has an inverse. You can easily check it out subtract two times the 2nd row from the third row you will end up in a all zero third row.
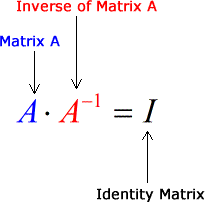
We look for an inverse matrix A 1 of the same size such that A 1 times A equals I. Note that AA1 is an m by m matrix which only equals the identity if m n. Section 23 A is invertible.
Right inverse If A has full row rank then r m. If it is if it does not Evan in verse. If the coefficient matrix does not have an inverse does that mean the system has no solution.
As we have seen when the rows of M are linearly dependent the equations that M defines do not have unique solutions which means that for some right hand sides there are lots of solutions and for some there are none. Let A be an nn matrix. If this number is non-zero then we must have an inverse.
A matrix is said to be singular or not invertible if it does not have an inverse. In the first case it is said to be singular and in the second case nonsingular. Then the following are equivalent.
If a matrix A has an inverse then A is said to be nonsingular or invertible. If the determinant of a matrix is 0 then the matrix has no inverse. If a metrics a has an inverse then it is cold in vertebral or non singular.
We saw a list of conditions in section 15 that can help us out. Their product is the identity matrixwhich does nothing to a vector so A 1Ax D x. Often you cant simply look at a matrix and tell whether it is invertible or not.
Whereas if this number is 0 we will not have an inverse. A square matrix is singular only when its determinant is exactly zero. The rows of A are independent.
What a matrix mostly does is to multiply. The matrix Y is called the inverse of X. A matrix X is invertible if there exists a matrix Y of the same size such that where is the n -by- n identity matrix.
Look at the numbers. For example if A is invertible then it is row-equivalent to I. Ax 0 has only the trivial solution.
In this video we will see why is that so. No singular metrics is the one in which the determinant is not equal to zero on continuing our question. To find the inverse of a square matrix A you need to find a matrix A 1 such that the product of A and A 1 is the identity matrix.
A singular matrix does not have an inverse. Consider the following matrix. And it makes sense.
A matrix does not have to have an inverse but if it does the inverse is unique. A matrix that has no inverse is singular. The following diagrams show how to determine if a 22 matrix is singular and if a 33 matrix is singular.
But A 1 might not exist. Such a matrix is called Singular which only happens when the determinant is zero. So how can we determine whether or not a given square matrix does actually have an inverse.
Scroll down the page for examples and solutions. A square matrix that has an inverse is called invertible or non-singular. The Attempt at a Solution I believe that I have to use the definition of invertible to do this.
If A and B are square matrices such that AB BA I the identity matrix then B is called the inverse of A and is denoted by A-1. Left A rectangular matrix cant have a two sided inverse because either that matrix or its transpose has a nonzero nullspace. Inverse Matrices 81 25 Inverse Matrices Suppose A is a square matrix.
The nullspace of AT contains only the zero vector. A matrix is said to be invertible or less commonly nonsingular if it has an inverse. We have found that instead of having to row reduce the entire matrix to determine if the matrix is invertible we can instead find the determinant of the matrix.
Yes it does mean that a matrix with no inverse cant be reduced to identity matrix in the elimination. However there are equivalent statements you should learn when A isis not invertible.

Zero Identity And Inverse Matrices Solutions Examples Videos Worksheets Games Activities

A Simple Condition For When The Matrix Inverse Exists Linear Algebra Makes Sense Youtube
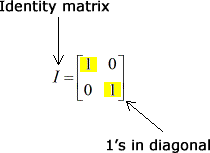
Inverse Of A 2x2 Matrix Chilimath
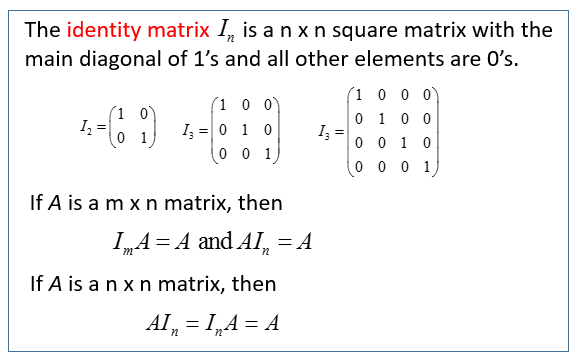
Zero Identity And Inverse Matrices Solutions Examples Videos Worksheets Games Activities
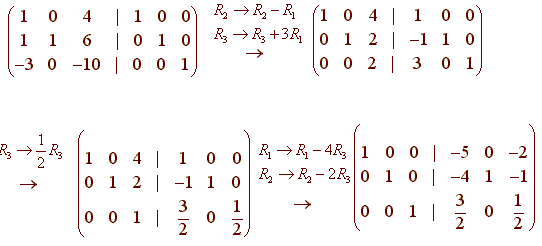
Inverse Of A Matrix Definition And Examples

Singular Matrix Video Lessons Examples And Solutions

Finding Inverses Of 2x2 Matrices Video Khan Academy

Zero Identity And Inverse Matrices Solutions Examples Videos Worksheets Games Activities
Inverse Of A 2x2 Matrix Chilimath

Inverse Matrices And Their Properties Youtube

What Is An Inverse Matrix Mathbootcamps
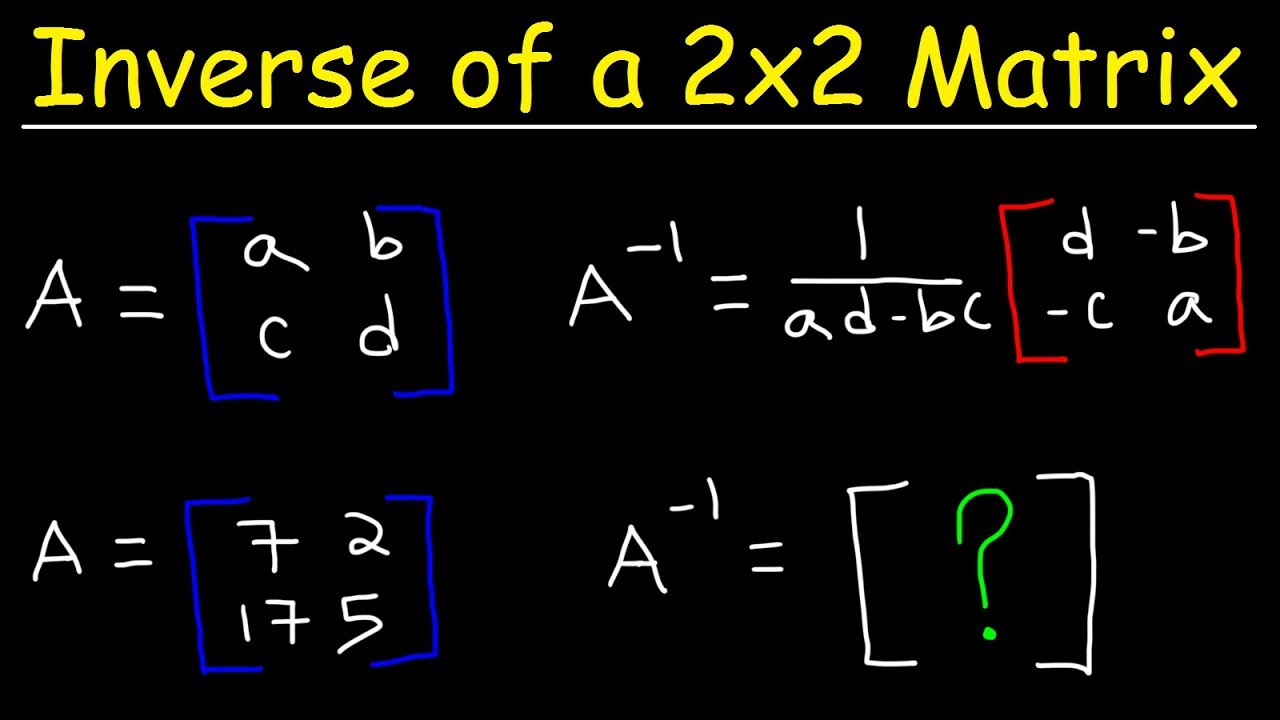
Inverse Of A 2x2 Matrix Youtube

What Is An Inverse Identity Matrix Quora

Inverse Of A 2x2 Matrix Chilimath

What Is An Inverse Matrix Mathbootcamps

Inverse Matrix Methods Formulas Solved Examples Of 2x2 And 3x3 Matrices
2 X 2 Invertible Matrix Studypug
