Matrix Vector Multiplication Runtime
Adaptive Runtime Tuning of Parallel Sparse Matrix-Vector Multiplication on Distributed Memory Systems Seyong Lee and Rudolf Eigenmann School of ECE Purdue University West Lafayette IN 47907 USA lee222eigenmanpurdueedu ABSTRACT Sparsematrix-vectorSpMVmultiplicationisawidelyused kernel in scienti c applications. A x a 11 a 12.
Multiplication Of Matrix Using Threads Geeksforgeeks
The fastest known matrix multiplication algorithm is Coppersmith-Winograd algorithm with a complexity of On 23737.
Matrix vector multiplication runtime. In these applications the. Our goal towards a universal library requires us to handle a multitude of matrix formats ranging from dense to multiple sparse encodings. There are several specialization methods and the best one depends both on the matrix and the platform.
Sal library is an FPGA-based matrix-vector multiplication MVM kernel which solves y Ax where x and y are vectors and A is a large matrix on the order of gigabytes or larger. INTRODUCTION Sparse Matrix Vector Multiplication SpMV is the kernel operation used in many iterative methods to solve large linear systems of equations. I have measured the runtime for a number of different vector length in this example there is only one number of elements N which is the length of the vector and at the same time defines the size of the matrix NxN and normalised the measured runtime to the number of elements.
In this paper we explore the potential for obtaining speedups for sparse matrix-dense vector multiplication using runtime specialization in the case where a single matrix is to be multiplied by many vectors. In 91-96 of the predictions either the best or the second best method is chosen. Runtime specialization is used for optimizing programs based on partial information available only at runtime.
To avoid having to generate all the specialization variations we use an autotuning approach to predict the best specializer for a given matrix. Adaptive Runtime Tuning of Parallel Sparse Matrix-Vector Multiplication on Distributed Memory Systems Seyong Lee and Rudolf Eigenmann School of ECE Purdue University West Lafayette IN 47907 USA lee222eigenmanpurdueedu ABSTRACT single-processor or shared memory systems 10 21. Where Aij is the i j th element of the matrix i 0 N 1 and bj is the j th element of the vector.
For a matrix of size N N and vector of size N matrixvector multiplication is given by Eq. Sparse matrix-vector multiplication SpMV of the form y Ax is a widely used computational kernel existing in many scientific applications. There Sparse matrix-vector SpMV multiplication is a widely used has been a focus on architecture-oriented.
Unless the matrix is huge these algorithms do not result in a vast difference in computation time. Cated runtime inspection module that can effectively reorder data 23 S. A 1 n a 21 a 22.
PhD thesis University of California Berkeley December 2003. 97 x i j 0 N 1 A i j b j. Let A be an n n sparse matrix that is block-distributed in a compressed sparse row-wise format 11 over the processors of an SIMD machine.
A 2 n a m 1 a m 2. In this paper we apply autotuning on runtime specialization of Sparse Matrix-Vector Multiplication to predict a best specialization method among several. It turns out that in many practical applications of matrix-vector multiplication the matrix mathbfA has some structure that potentially allows one to perform matrix vector multiplication asymptotically faster than Omegan2 time.
13 1 Article 5 March 2016 26 pages. Autotuning runtime specialization for sparse matrix-vector multiplication. The general formula for a matrix-vector product is.
In practice it is easier and faster to use parallel algorithms for matrix multiplication. In the case of a repeated y Ax operation involving the same input matrix A but possibly changing numerical values of its elements A can be preprocessed to reduce both. Runtime specialization is used for optimizing programs based on partial information available only at run-time.
We experiment with five methods involving runtime specialization comparing them to methods that do not including Intels MKL library. In this paper we apply autotuning on runtime specialization of Sparse Matrix-VectorMultiplication to predict a best specialization method among several. The multiplication is done several times to get a reliable estimate of the runtime.
Let x be a vector aligned with the columns of A and iteratively updated according to the equation xj1 Axj. To execute matrix-vector multiplication it is necessary to execute m operations of inner multiplication. Algorithms for run-time optimization of iterative sparse matrix-vector multiplication on SIMD machines.
Quickly specialize Sparse Matrix-Vector Multiplication code for a particular matrix at runtime. A m n x 1 x 2 x n a 11 x 1 a 12 x 2 a 1 n x n a 21 x 1 a 22 x 2 a 2 n x n a m 1 x 1 a m 2 x 2 a m n x n. Matrix-vector multiplication is the sequence of inner product computations.
The challenges are two-fold. To this end we de ne a set of matrix features for autotuning. As each computation of inner multiplication of vectors of size n requires execution of n multiplications and n-l additions its time complexity is the order On.
The input matrix A is sparseThe input vector x and the output vector y are dense. Thus the algorithms time complexity is the order Omn. In 91 to 96 of the predictions either the best or the second-best method is chosen.
And computation to further exploit data reuse and optimize mem- Optimization of sparse matrix-vector multiplication on emerging ory access.
Hierarchical Matrix Operations On Gpus Matrix Vector Multiplication And Compression
Computational Complexity Of Matrix Vector Product Mathematics Stack Exchange
Matrix Multiplication Using The Divide And Conquer Paradigm
Vectorization How To Speed Up Your Machine Learning Algorithm By X78 By Ioannis Gatopoulos Towards Data Science
Time Complexity Of Some Matrix Multiplication Mathematics Stack Exchange
Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
Matrix Vector Multiplication Optimisation Cache Size Stack Overflow
Dense Matrix Algorithms Topic Overview Matrix Vector Multiplication Matrix Matrix Multiplication Solving A System Of Linear Equations Ppt Download
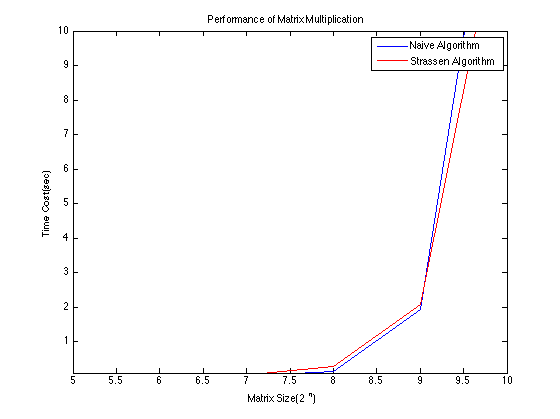
Strassen S Matrix Multiplication Algorithm
1 Complexity Of Bidiagonal Reduction Algorithms Download Table
C Code That Constructs A Matrix Multiplication And Transforms It With Download Scientific Diagram
Vector Multiplication An Overview Sciencedirect Topics
Strassen S Matrix Multiplication Algorithm
Numerical Algorithms Matrix Multiplication Ppt Download
Hierarchical Matrix Operations On Gpus Matrix Vector Multiplication And Compression
Beyond Word Embeddings Part 2 Word Vectors Nlp Modeling From Bow To Bert Nlp Computational Linguistics Deep Learning
