Matrix Block Multiplication Inverse
Multiplying block matrices. Elementary Matrices We introduce elementary matrices and demonstrate how multiplication of a matrix by an elementary matrix is equivalent to to performing an elementary row.
Multiplying Matrices Youtube
Matrix operations on block matrices can be carried out by treating the blocks as matrix.
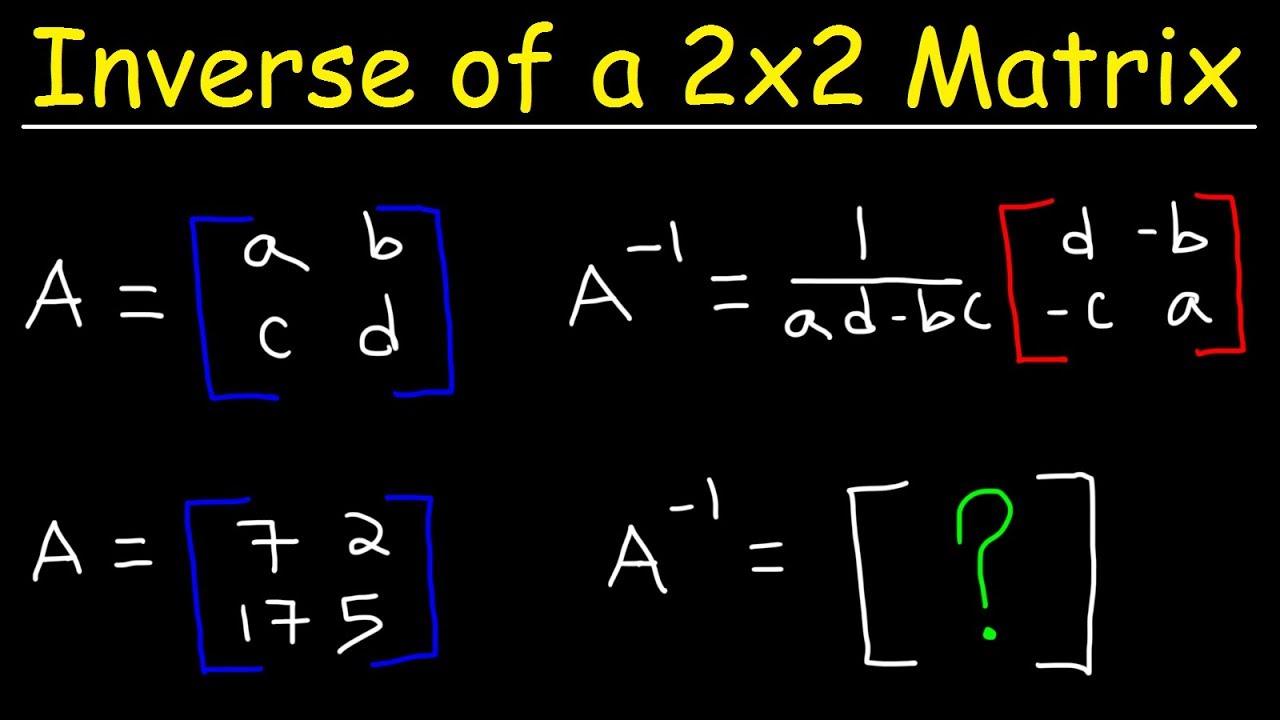
Matrix block multiplication inverse. If a matrix A has an inverse then it is said to be invertible or non-singular. 21 To make the multiplication of R by R -1 and R -1 by R possible the sizes of all blocks cannot be arbitrary. In fact if A-1 is the inverse matrix of a square matrix A then its both the left-inverse and the right inverse ie A-1 A AA-1 I.
Block Matrix Multiplication - 1819. They want us to verify by block multiplication that the inverse of a matrix if partitioned as shown is as claimed assume that all inverses exist as needed. Using this package you would find the block inverse of the example matrix using.
Which has the special case. Then to the right will be the inverse matrix. Where In denotes the n-by-n identity matrix and the multiplication used is ordinary matrix multiplication.
A useful formula for the inverse of a nonsingular block triangular matrix. 11 11 A A 12 A 21 A 22 22 jA jjF 11j jA jjF. Gauss-Jordan Elimination - 3539.
We develop a method for finding the inverse of a square matrix discuss when the inverse does not exist and use matrix inverses to solve matrix equations. Inverse Matrix - 2121. To be invertible a matrix must be square because the identity matrix must be square as well.
Inverse NCInversematrix Out inva -inva b invd 0 invd Here inva represents the general inverse of the a block of the matrix and the represents non-commutative ie. In doing exercise 1610 in Linear Algebra and Its Applications I was reminded of the general issue of multiplying block matrices including diagonal block matrices. MATLAB TUTORIAL- How to find Matrix inverse using MATLAB Simulink.
Left begin array cccc2 1 1 01 3 0 1end arrayright. If this is the case then the matrix B is uniquely determined by A and is called the inverse of A denoted by A1. Let a matrix be partitioned into a block form.
This approach works for larger 3x3 4x4 etc square block matrices as well. The proof is easy. 09 block matrices for conformably partitioned block matrices addition and multiplication is performed by adding and multiplying blocks in exactly the same way as scalar elements of regular matrices however determinants and inverses of block matrices are very tricky.
Inverse of Square Matrix - 2127. The matrixA1is called Ainverse. So augment the matrix with the identity matrix.
This means simply that the matrix does not have an inverse. Note the first and the last columns are equal. Where the matrix andmatrix are invertible.
A square matrix that is not invertible is called singular or degenerate. Computer theorem proving of matrix theory. Matrix inversion is the process of finding the matrix B that satisfies the prior equation for a given invertible matrix A.
To find the inverse matrix augment it with the identity matrix and perform row operations trying to make the identity matrix to the left. The matrix is not invertible. A number has an inverse if it is not zeromatrices are more complicated and more interesting.
Therefore when we try to find the determinant using the following formula we get the determinant equaling 0. If is upper triangular then so are and By taking of dimension the nearest integer to this formula can be used to construct a divide and conquer algorithm for computing. We then learn how to find the inverse of a matrix using elimination and why the Gauss-Jordan method works.
Let a matrix be partitioned into a block form. Then after this partition the matrix below so that you can apply the formula acquired from the above exercise to calculate the inverse. An inverse of a matrix A is another matrix such that A-1 A I where I is the identity matrix.
For 2 blocks by 2 blocks the results are. This also came up in exercise 1424 as well which I answered without. INVERSE FORMULAE A nonsingular square matrix R and its inverse R -1 can be partitioned into 2 x 2 blocks as R A D B and R_ 1 E FH.
For example if there are large blocks of zeros in a matrix or blocks that look like an identity matrix it can be useful to partition the matrix accordingly. To determine the inverse of the matrix 3 4 5 6 set 3 4 5 6a b c d 1 0 0 1. It can be proved that the above two matrix expressions for are equivalent.
The productA1Ais like multiplying by number and then dividing by that number. Matrix A is singular if we can find a non-zero vector x such that Ax 0. These video lectures of Professor Gilbert Strang teaching 1806 were recorded in Fall 1999 and do not correspond precisely to the current edition of the textbook.
The definition of a matrix inverse requires commutativitythe multiplication must work the same in either order. This lecture looks at matrix multiplication from five different points of view. Context or the entries of the matrix will suggest a useful way to divide the matrix into blocks.
We note that a fact that will be used in the next section. Then the inverse of is.
Chapter 2 Matrices 2 1 Operations With Matrices
Matrix Inverse
Matrix Multiplication With A Transpose Example Youtube
Inverse Matrices And Their Properties Youtube
Determinants Matrices A Matrix Is An Array Of
Inverse Of A 2x2 Matrix Chilimath
Matrix Google Search Learning Mathematics Mathematics Polynomials
Pin On Math Classroom Activities
Left Inverse And Right Matrix Inverses Youtube
Problems 1 Determine Whether Each Matrix Is Chegg Com
Pin On Matrices
6 4 Inverse Matrices T
Generalized Inverse Of 2 X 2 Block Matrix Mathematics Stack Exchange
Inverse And Block Multiplication Mathematics Stack Exchange
6 4 Inverse Matrices T
Pin On Multiplicative Inverse Determinant
If You Multiply A 1x2 Matrix By A 2x1 Matrix What Are The Dimensions Of The Resulting Matrix Quora
Inverse Matrices And Their Properties Youtube
Inverse Of A 2x2 Matrix Chilimath
